Do it! 강화학습 입문 1장_1

January 18, 2022 8 분 소요

이번 포스팅 부터 Do it! 강화학습 입문을 정리해서 올릴 예정이며 해당 포스팅은 1편입니다.

머신러닝 안에서 강화학습, 지도학습, 비지도 학습의 관계

지도 학습이란?

지도 학슴은 데이터와 각 데이터의 레이블이 주어진 상태에서 새 데이터 레이블을 매기는 방법으로 학습하는 것 입니다. 지도학습은 문제와 정답을 모델에게 알려주는 방식으로 진행되며 주로 회귀를 이용한 문제 예측 에서 주로 사용 됩니다.

비지도 학습이란?

비지도 학습은 레이블 없이 데이터만 주어진 상태에서 데이터를 분류하거나 밀도를 추정하는 방법을 학습하는 것 입니다. 즉 비지도 학습은 데이터의 특징을 요약할때 사용합니다. 유사한 몇 가지 군집으로 분류해서 상품을 추천하려고 한다면 비지도 학습을 이용 할 수 있습니다.

강화 학습이란?

지도 학습, 비지도 학습과 달리 강화 학습은 행동에 대한 보상만 주어집니다. 그런데 강화 학습에서 풀어야 하는 문제는 행동-보상의 짝이 아니라 상태에 대한 행동을 찾는 것입니다. 우리가 인공지능에 무엇을 해주기를 바랄때 단순하면서도 반복되는 다양한 잡무를 빠르게 처리하는것은 인공지능이 아닌 컴퓨터로도 얼마든지 할 수 있을 것 입니다. 이제 기계에게 컴퓨팅을 뛰어넘어 사람만이 할 수 있는 판단, 창작, 의사 결정과 같은 작업을 해주길 기대할때 강화 학습을 이용 할 수 있습니다.

마르코프 결정 과정으로 시작하는 강화 학습

의사 결정을 수행하는데 있어서 사용하는 특성 중에 마르코프 결정 과정(MDP)이 있습니다. 영화 “엣지 오브 투모로우”에서 그 모델을 보여주는데에 좋은 예시가 될수 있습니다.

상태, 행동, 보상 정리하기

에이전트는 시작 상태와 종단 상태를 포함하여 총 7가지 상태를 가질 수 있는데 그 행동에 대한 보상은 다음과 같습니다.
예): 부정종단 R(s3) = -1, R(s4) = -1, 긍정종단 R(s7) = 1, 종단상태 제외 R(s1) = 0, R(s2) = 0, R(s5) = 0, R(s6) = 0

행동에 의한 상태전이에 확률 도입하기

에이전트가 s1에서 행동a1-2를 취하면 상태가 완전히 s5로 바뀔 것인가? 하면 그렇지 않습니다. 실제 현실에서도 행동에 대한 결과가 100% 발현 되지 않듯이 80%확률로는 s5로 20%확률로 s1으로 전이 될 수도 있습니다. 상태 행동 한 싸의 전이 확률의 합은 1이 됩니다.
p(s1, a1-2) = 0.8
p(s1, a1-2) = 0.2

에이전트의 상황을 상태, 행동, 보상, 모델 이라는 4가지 요소로 정리하여 의사 결정을 하는데 이용합니다.

상태(Status, S)	에이전트가 환경 내 특정 시점에서 관찰 할 수 있는 것을 수치화
행동(Action, A)	에이전트가 환경에게 전달하는 입력
보상(Reward, R)	에이전트가 환경으로부터 전달받은 목적을 달성하기 위해 행동을 잘 수행하고 있는지를 피드백하는 신호
모델(Model, M)	행동에 따른 상태 전이가 일어날 확률을 담은 규칙

MDP는 상태 집합 S로 이루어지며 행동집합 A가 있고, 상태 s에서 행동 a를 통해 상태 s’로 전이할 확률은 P(s’|s,a)이며, 그 보상은 R(s,a)가 됩니다. 여기서 MDP는 에이전트가 지나온 상태 또는 행동과 어떤 연관이 있지 않을까? 생각 할 수 있지만 MDP는 확률이 달라지지 않습니다. 즉 에이전트가 이전에 어떤 상태를 지나왔는지는 중요하지 않고 오직 현재 상태만 다음 상태 전이 확률에 영향을 미칩니다.

보상 총합이 무한으로 발산하는 문제?

상태 경로와 보상 총합을 표현에 놓고 보면 상태 변경 횟수에 제약을 받지 않고 무한이 구간을 반복하는 문제가 발생 할 수 있습니다. 이때는 시간에 따른 할인 개념을 도입하여 해결 할 수 있습니다. 최대한 가까운 시점에 보상을 얻게 하는 장치를 마련하면 보상에 할인율을 점차 곱해 더하는 방식으로 보상의 총합을 구하는 것 입니다. 할인율은 0보다 크고 1보다 작으며 이를 수식에서 감마γ 로 표현합니다.

주어진 상태에서 미래를 얻을 수 있는 보상 총합 알아보기

우리는 주어진 상태에서 최적의 행동을 찾는 방법이 필요합니다. 따라서 한 에피소드에서 얻을 수 있는 보상 총합이 아니라 주어진 상태에서 미래에 얻을 수 있는 보상의 총합을 구해야합니다. 이를 수식으로 표현하면 할인율과 t번째 상태로 다음과 같이 타나내면 이익이라는 표현을 사용합니다.

보상, 이익, 가치 함수 개념 정리

지금까지의 보상, 이익, 가치함수의 개념을 정리해 보면 아래와 같습니다.

보상(R)	특정 상태에서 얻을 수 있는 즉각적인 피드백
이익(G)	한 에피소드의 특정 상태에서 종단 상태까지 받을 수 있는 보상 총합
가치 함수(V)	특정 상태로부터 기대할 수 있는 보상

보상과 가치 함수의 차이는 실생활에서 만약에 예방 주사를 맞을때 병원비와 아픔을 생각하면 즉각적인 보상은 음수가 됩니다. 하지만 장기적으로는 건강이라는 가치를 제공함으로 이는 양수라 할 수 있습니다.

가치 직접 구해 보기

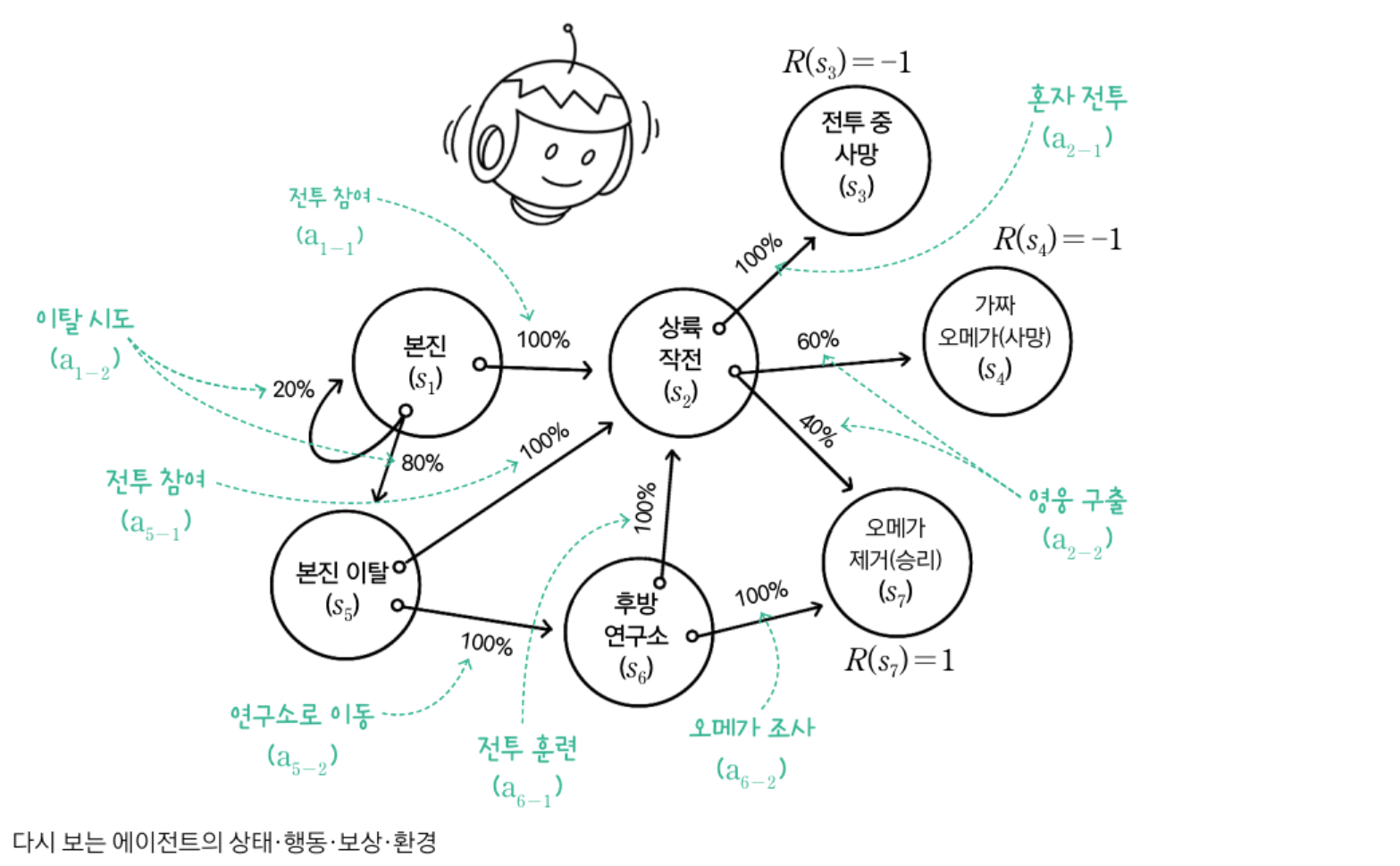
보상이 종단상태에는 적혀 있지만 다른 상태에는 적혀있지 않습니다. 종단 상태를 제외한 모든 상태의 가치를 0으로 초기화 합니다. 종단 상태는 더 이상 전이가 없으니 보상은 곧 가치이므로 V(s3)=-1, V(s4)=-1. V(s7)=1 입니다.
다음은 인접한 상태 s2의 가치를 구해봅니다. s2의 가치는 s2에서 이동할 수 있는 행동의 기대 가치에 할인율을 곱한 다음, 현재 보상을 더해 구하면 됩니다. 다음은 할인율을 0.9로 가정해서 구한 s2의 가치입니다.

이 표를 참고하여 s2에 취할 수 있는 행동 a2-1, a2-2에서 가치의 기댓값을 비교해 보면 a2-2가 -0.18, a2-1이 -0.9이므로 전자가 더 크다는 걸 알 수 있습니다. 이제 가치를 구할 수 있는데 s2자체 보상은 0이므로 s2의 가치는 기댓값 -0.9에 현재 보상 0을 더해 -0.9임을 알 수 있습니다.

현재 상태의 가치를 구해 주는 벨만 방정식

앞의 과정을 벨만 방정식으로 표현 할 수 있습니다. 벨만 방정식은 다음 상태의 가치로 현재 상태의 가치를 구합니다. 현재 상태의 가치를 구하려고 다음 상태를 계속 추적하므로 결국 종단 상태에 도달합니다. 이 방식으로 다음 상태를 따라가면 결국 종단 상태의 가치로 상태를 역추적하여 계산하게 됩니다. 종단 상태의 가치는 종단 상태의 보상과 같으므로 이미 알려진 값이 되는 것입니다. 이를 코드로 구현하려면 동적 계획법 알고리즘을 사용해야 합니다.

종단 상태를 제외한 모든 상태의 가치 V(s)를 0으로 초기화
반복 카운터 n을 0으로 초기화
반복:

    반복 카운터 n을 1증가
    모든 상태 s에 대해 반복:
        상태 s에서 취할 수 있는 모든 행동 a에 대해 반복:
            s에서 a를 취할 때의 모든 상태 전이 확률 P(s'|s, a)를 확인
            s에서 a를 선택해 도닥하는 다음 상태 s'의 가치 V(s')와 P(s'|s,a)를 곱함
            도달 가능한 모든 상태 s'에 대해 P(s'|s, a) X V(s')를 합산한 기댓값을 구함
        모든 행동 a중 기댓값이 가장 큰 최적 행동 a를 확인
    a의 기댓값에 할인율 γ를 곱하고, 상태 s의 보상 R(s)를 더한 값 Vn(s)를 구함
    모든 s에 대해 Vn(s) - Vn-1(s)가 0을 만족하면 반복을 종료

이러한 모든 상태 가치를 구하고 이를 바탕으로 행동을 취하게 됩니다. 이렇게 함수를 모두 구하면 각 상태에 대해 미래 보상을 최대화 하는 최적 행동을 선택 할 수 있습니다. 즉 상태를 입력으로 받아 최적 행동을 출력하는 함수가 만들어 집니다. 이러한 함수를 정책 이라 하는데 이 정책이 바로 강화 학습에서 구하고자 하는 목표입니다.

강화 학습의 목표, 정책

정책이란 지금 상태에서 해야 할 최적의 행동이 무엇인지를 알려주는 것 이고 가치 반복법을 통해 수렴한 가치 함수는 최적의 가치 함수가 극대화되는 행동 a를 찾으면 됩니다. 벨만 방적식을 수식으로 표현할 수 있는데 이는 아래와 같습니다.

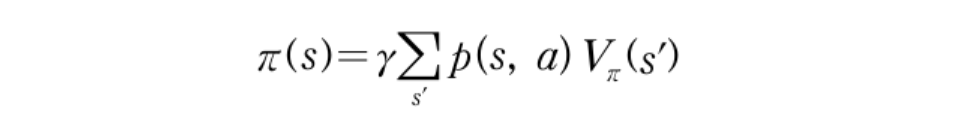
지금까지 예로 든 “엣지 오브 투모로우”의 MDP는 4번만 반복하면 상태에 대한 가치 함수가 더이상 업데이트 되지 않고 수렴합니다. 하지만 복잡한 MDP는 가치 함수를 훨씬 많이 반복해서 업데이트 해야 하는데 모든 상태의 가치가 수렴되기까지 반복하기 보다는 가치 갱신값 차이가 일정한 임계값 이내에 들어오면 반복을 종료하는 방식을 사용하기도 합니다.

정책 평가와 정책 개선

정책은 처음에 무작위로 초기화합니다. 정책이 주어진 것은 에이전트가 어떤 상황에서 어떤 행동을 해야 할지 지시 받았음을 의미합니다. 앞서 살펴본 반봅법과 차이가 있다면 상태 s에서 선택할 수 있는 모둔 행동에 대해 이익의 기댓값을 계산하고 최대치를 고르는 것이 아니라, 주어진 행동에 대한 이익의 기댓값만 계산하면 된다는 점 입니다. 이렇게 주어진 정책에 따라 가치 함수를 정책 평가라 합니다.

격자 세계로 알아보는 가치 반복법

다음과 같은 격자 공간에 초기 상태와 종단 상태가 주어집니다. 이중 도달 할 수 업는 구역도 존재하며 (0,0)에서 상하 좌우 네 방향으로 움직일 수 있습니다.

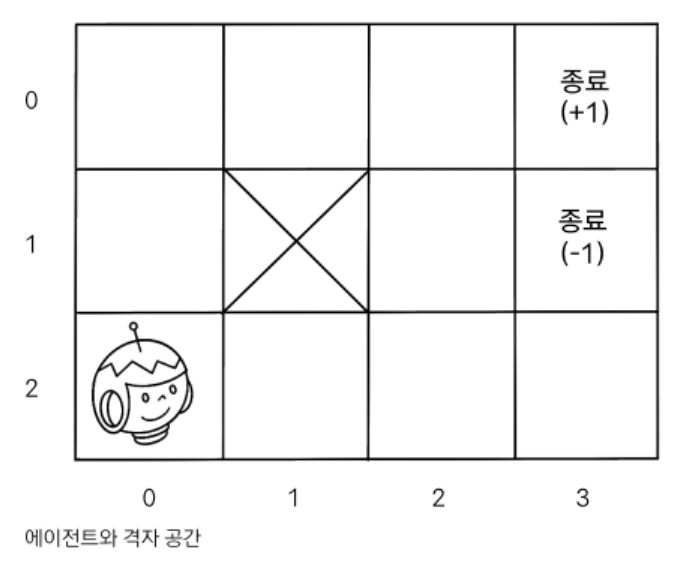
에이전트가 행동을 선택하면 의도한 대로 상태 전이가 이루어질 확률은 80%, 의도한 방향의 반대로 이루어질 확률은 0% 의도하지 않은 나머지 두 방향으로 이루어질 확률은 각각10%입니다.

가치 반복법 구현하기

import numpy as np

ACTIONS = ('U', 'D', 'L', 'R')
DELTA_THRESHOLD = 1e-3
GAMMA = 0.9

# 격자 공간의 클래스를 정의
class Grid: 
	def __init__(self, rows, cols, start):
		self.rows = rows
		self.cols = cols
		self.i = start[0]
		self.j = start[1]

	# 각 상태의 보상과 선택 가능한 행동을 설정
	def set(self, rewards, actions):
		self.rewards = rewards
		self.actions = actions

	def set_state(self, s):
		self.i = s[0]
		self.j = s[1]

	def current_state(self):
		return (self.i, self.j)

	def is_terminal(self, s):
		return s not in self.actions

	def move(self, action):
		if action in self.actions[(self.i, self.j)]:
			if action == 'U':
				self.i -= 1
			elif action == 'D':
				self.i += 1
			elif action == 'R':
				self.j += 1
			elif action == 'L':
				self.j -= 1
	    # 보상이 있을 경우 보상을 반환
		return self.rewards.get((self.i, self.j), 0)

	# 모든 상태를 반환
	def all_states(self):
		# possibly buggy but simple way to get all states
		# either a position that has possible next actions
		# or a position that yields a reward
		return set(self.actions.keys()) | set(self.rewards.keys())

# 격자 공간과 각 상태에서 선택 가능한 행동을 정의
def standard_grid():
	grid = Grid(3, 4, (2, 0))
	rewards = {(0, 3): 1, (1, 3): -1}
	actions = {
		(0, 0): ('D', 'R'),
		(0, 1): ('L', 'R'),
		(0, 2): ('L', 'D', 'R'),
		(1, 0): ('U', 'D'),
		(1, 2): ('U', 'D', 'R'),
		(2, 0): ('U', 'R'),
		(2, 1): ('L', 'R'),
		(2, 2): ('L', 'R', 'U'),
		(2, 3): ('L', 'U'),
	}
	grid.set(rewards, actions)
	return grid

def print_values(V, grid):
	for i in range(grid.rows):
		print("---------------------------")
		for j in range(grid.cols):
			value = V.get((i, j), 0)
			if value >= 0:
				print("%.2f | " % value, end = "")
			else:
				print("%.2f | " % value, end = "") # -ve sign takes up an extra space
		print("")

def print_policy(P, grid):
	for i in range(grid.rows):
		print("---------------------------")
		for j in range(grid.cols):
			action = P.get((i, j), ' ')
			print("  %s  |" % action, end = "")
		print("")

if __name__ == '__main__':
    # 격자 공간을 초기화
	grid = standard_grid()

	# 보상을 출력
	print("\n보상: ")
	print_values(grid.rewards, grid)

	# 초기 정책은 각 상태에서 선택 가능한 행동을 무작위로 선택
	policy = {}
	for s in grid.actions.keys():
		policy[s] = np.random.choice(ACTIONS)

	# 정책 초기화
	print("\n초기 정책:")
	print_policy(policy, grid)

	# 가치 함수 V(s) 초기화
	V = {}
	states = grid.all_states()
	for s in states:
		# V[s] = 0
		if s in grid.actions:
			V[s] = np.random.random()
		else:
			# 종단 상태
			V[s] = 0

	# 수렴할 때까지 반복
	i = 0
	while True:
		maxChange = 0
		for s in states:
			oldValue = V[s]

			# 종단 상태가 아닌 상태에 대해서만 V(s)를 계산
			if s in policy:
				newValue = float('-inf')
				for a in ACTIONS:
					grid.set_state(s)
					r = grid.move(a)
					# 벨만 방정식 계산
					v = r + GAMMA * V[grid.current_state()]
					if v > newValue:
						newValue = v
				V[s] = newValue
				maxChange = max(maxChange, np.abs(oldValue - V[s]))

		print("\n%i  번째 반복" % i, end = "\n")
		print_values(V, grid)
		i += 1 

		if maxChange < DELTA_THRESHOLD:
			break

	# 최적 가치 함수를 찾는 정책을 도출
	for s in policy.keys():
		bestAction = None
		bestValue = float('-inf')
		# 가능한 모든 행동에 대해 반복
		for a in ACTIONS:
			grid.set_state(s)
			r = grid.move(a)
			v = r + GAMMA * V[grid.current_state()]
			if v > bestValue:
				bestValue = v
				bestAction = a
		policy[s] = bestAction

	# 계산된 가치 함수와 정책을 출력
	print("\n가치 함수: ")
	print_values(V, grid)

	print("\n정책: ")
	print_policy(policy, grid)

실행 결과는 아래와 같습니다.

Twitter Facebook LinkedIn

ParkYongYeon