백준 - 특정 거리의 도시 찾기[18352] (다익스트라)

이번 포스팅에서는 백준 알고리즘의 특정 거리의 도시 찾기[18352] (다익스트라) 코딩테스트 연습 문제를 풀어봅니다.

문제 설명

어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.

이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 가정한다.

예를 들어 N=4, K=2, X=1일 때 다음과 같이 그래프가 구성되어 있다고 가정하자.

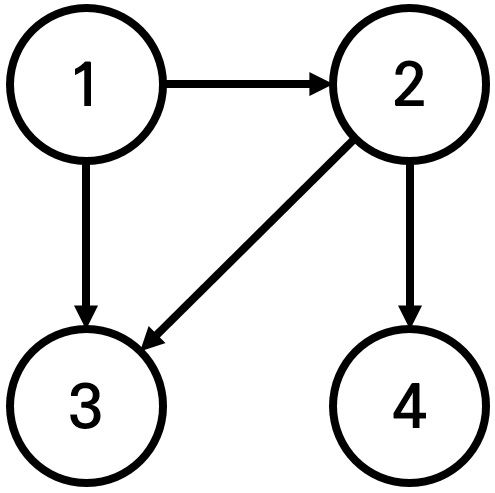
이 때 1번 도시에서 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.

입력

첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개의 자연수 A, B가 공백을 기준으로 구분되어 주어진다. 이는 A번 도시에서 B번 도시로 이동하는 단방향 도로가 존재한다는 의미다. (1 ≤ A, B ≤ N) 단, A와 B는 서로 다른 자연수이다.

출력

X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력한다.

이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.

입출력 예

입력	출력
4 4 2 1 1 2 1 3 2 3 2 4	4
4 3 2 1 1 2 1 3 1 4	-1
4 4 1 1 1 2 1 3 2 3 2 4	2 3

문제 풀이

다른 노드까지의 최단 경로를 구하는 다익스트라 알고리즘을 사용 하여 문제를 해결 합니다.

먼저 방문 배열과 비용&거리 배열을 선언 하고 X도시의 시작점으로 설정 하여 cost[X-1] 노드의 거리 비용을 0으로 합니다.

def solution(N, M, road, K, X):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    cost[X-1] = 0   # X 도시를 시작 점으로 지정
    
solution(4, 4, [[1, 2], [1, 3], [2, 3], [2, 4]], 2, 1)

방문 배열이 모두 True가 될때 까지 루프를 지속합니다. 먼저 방문하지 않은 지역 중 최솟값을 찾고 더이상 검사할 후보가 없다면 루프를 종료 합니다.

def solution(N, M, road, K, X):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    cost[X-1] = 0   # X 도시를 시작 점으로 지정
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        checkLoc = -1 # 방문하지 않은 지역 중 최솟값 찾기
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break

solution(4, 4, [[1, 2], [1, 3], [2, 3], [2, 4]], 2, 1)

검사할 대상의 방문 배열을 True로 변경하고 road 리스트의 값을 통해 경로 완전탐생을 수행하고 비용 배열의 값을 수정합니다.
루프가 모두 완료 되면 X도시에서 각 도시 까지의 최단 경로 시간을 얻을 수 있습니다.

def solution(N, M, road, K, X):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    cost[X-1] = 0   # X 도시를 시작 점으로 지정
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        checkLoc = -1 # 방문하지 않은 지역 중 최솟값 찾기
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break
        visited[checkLoc] = True # 검사할 대상의 방문 배열을 True로 변경
        for v1, v2 in road:  # 경로 완전탐색으로 비용배열 수정
            v1 -= 1 # 방문 및 비용 배열은 0부터 시작 함으로 도시 번호를 -1씩 빼고 계산
            v2 -= 1
            if v1 == checkLoc and visited[v2] == False: # 검사할 대상과 road배열의 값과 일치 하고 연결된 도시가 방문한 노드가 아니라면
                cost[v2] = min(cost[v2], cost[v1] + 1)  # 연결된 도시의 거리 비용 값을 두개의 값(기존 값, 검사할 대상의 거리 비용 값과 거리 시간 값)을 비교한 값 중 작은 값으로 변경
    print(cost)

solution(4, 4, [[1, 2], [1, 3], [2, 3], [2, 4]], 2, 1)

[0, 1, 1, 2]

거리 비용 배열에서 거리 비용이 K 값과 일치 하는 도시를 출력 합니다. 값이 없다면 -1을 출력합니다.
예제 입력을 추가하여 확인 해 보았습니다.

def solution(N, M, road, K, X):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    cost[X-1] = 0   # X 도시를 시작 점으로 지정
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        checkLoc = -1 # 방문하지 않은 지역 중 최솟값 찾기
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break
        visited[checkLoc] = True # 검사할 대상의 방문 배열을 True로 변경
        for v1, v2 in road:  # 경로 완전탐색으로 비용배열 수정
            v1 -= 1 # 방문 및 비용 배열은 0부터 시작 함으로 마을 번호를 -1씩 빼고 계산
            v2 -= 1
            if v1 == checkLoc and visited[v2] == False: # 검사할 대상과 road배열의 값과 일치 하고 연결된 마을이 방문한 노드가 아니라면
                cost[v2] = min(cost[v2], cost[v1] + 1)  # 연결된 마을의 거리 비용 값을 두개의 값(기존 값, 검사할 대상의 거리 비용 값과 거리 시간 값)을 비교한 값 중 작은 값으로 변경

    if sum(K == cost[i] for i in range(length)): # 거리 비용 배열에서 K 시간과 일치 하는 도시가 존재 하면
        for i in range(M):    # 도시를 출력
            if cost[i] == K:
                print(i+1)
    else:
        print(-1)

solution(4, 4, [[1, 2], [1, 3], [2, 3], [2, 4]], 2, 1)
solution(4, 3, [[1, 2], [1, 3], [1, 4]], 2, 1)
solution(4, 4, [[1, 2], [1, 3], [2, 3], [2, 4]], 1, 1)

4
-1
2
3

마지막으로 백준 문제에 맞게 입력을 받아서 처리하도록 수정 합니다.

from sys import stdin
# 입력
N, M, K, X = map(int,stdin.readline().split())
road = []
for i in range(M):
    road.append(list(map(int, stdin.readline().split())))

# 연산
visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    cost[X-1] = 0   # X 도시를 시작 점으로 지정
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        checkLoc = -1 # 방문하지 않은 지역 중 최솟값 찾기
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break
        visited[checkLoc] = True # 검사할 대상의 방문 배열을 True로 변경
        for v1, v2 in road:  # 경로 완전탐색으로 비용배열 수정
            v1 -= 1 # 방문 및 비용 배열은 0부터 시작 함으로 마을 번호를 -1씩 빼고 계산
            v2 -= 1
            if v1 == checkLoc and visited[v2] == False: # 검사할 대상과 road배열의 값과 일치 하고 연결된 마을이 방문한 노드가 아니라면
                cost[v2] = min(cost[v2], cost[v1] + 1)  # 연결된 마을의 거리 비용 값을 두개의 값(기존 값, 검사할 대상의 거리 비용 값과 거리 시간 값)을 비교한 값 중 작은 값으로 변경

    if sum(K == cost[i] for i in range(length)): # 거리 비용 배열에서 K 시간과 일치 하는 도시가 존재 하면
        for i in range(M):    # 도시를 출력
            if cost[i] == K:
                print(i+1)
    else:
        print(-1)

하지만 위의 코드는 시간 초과가 발생 합니다.

방식 자체는 틀리지 않지만 모든 노드의 최단 거리 값을 계산 하는 다익스트라 알고리즘의 특성상 노드의 숫자가 많아지면 계산하는데 필요한 연산이 많아 질 수 밖에 없습니다.

다익스트라의 이러한 점을 개선한 “A star”알고리즘이 존재 하지만 “A star” 알고리즘은 포스팅에서 개념 정리 후 다른 문제에서 사용해 보겠습니다.

이번 문제에 더 적합한 방법은 무엇 일까요? 바로 BFS 탐색 알고리즘을 이용하는 것 입니다. 이번 문제의 특징은 방향성이 존재하고 거리 값이 1로 고정 되어 있습니다. 이는 BFS 알고리즘이 좀 더 유리하며 만약에 거리 값이 1이 아닌 주어진 값을 이용 한다면 다익스트라 알고리즘이 유리 할 것 입니다.

그러면 방문하지 않은 지역 중 최솟값 찾기 부분을 연결된 노드 중에 BFS탐색 알고리즘 방식으로 큐를 추가 하여 검색하는 방법으로 처리 방식을 수정 합니다.

import sys; input = sys.stdin.readline
from collections import deque
# 입력
N, M, K, X = map(int,input().split())
road = {}
for i in range(M): # 2번째 인자값인 간선의 개수만큼 리스트 추가
    p1, p2 = map(int, input().split())
    try: road[p1].append(p2) # 정점과 연결된 다른 노드를 리스트를 딕셔너리 형태로 저장
    except: road[p1] = [p2]

# 연산
visited = [False for _ in range(N+1)]  # 방문 배열 선언
cost = [2**31-1 for _ in range(N+1)]  # 비용 배열, 거리 배열 선언
cost[X] = 0     # 출발할 노드의 값을 0으로 설정

checkNode = deque()
checkNode.append(X) # 첫번째 탐색 값을 큐에 등록
while checkNode:
    now = checkNode.popleft()
    visited[now] = True
    try: next = road[now] # 연결된 노드가 존재 하면 next에 리스트 선언
    except: next = [] # 연결된 노드가 더이상 존재 하지 않으면 빈 리스트 선언
    for node in next:
        if visited[node] == False:
            cost[node] = min(cost[node], cost[now] + 1)
            checkNode.append(node)

result = []
for i in range(N+1):
    if cost[i] == K:
        result.append(i)
if result:
    result.sort()
    for r in result:
        print(r)
else:
    print(-1)

결과는 아래와 같이 잘 통과 되는 것을 확인 할 수 있습니다.