프로그래머스 - 가장 먼 노드 (다익스트라)

이번 포스팅에서는 프로그래머스의 가장 먼 노드 (다익스트라) 코딩테스트 연습 문제를 풀어봅니다.

문제 설명

n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.

노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.

제한사항

• 노드의 개수 n은 2 이상 20,000 이하입니다.
• 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
• vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.

입출력 예

n	vertex	return
6	[[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]	3

입출력 예 설명

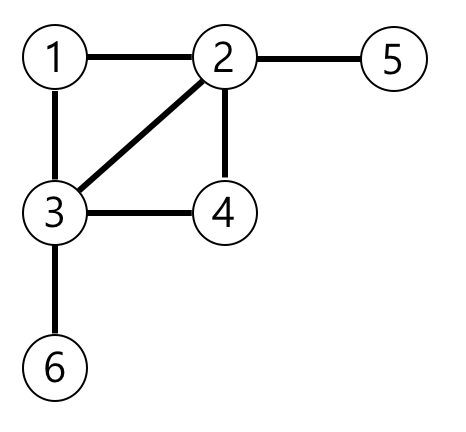
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.

문제 풀이

다른 노드까지의 최단 경로를 구하는 다익스트라 알고리즘을 사용 하여 문제를 해결 합니다.

먼저 특정 노드와 연결된 다른 노드의 정보를 쉽게 확인 할 수 있도록 딕셔너리를 이용하여 정렬 합니다.

def solution(N, edge):
    vertex = {}
    for e in edge:
        try: vertex[e[0]].append(e[1])
        except: vertex[e[0]] = [e[1]]
        try: vertex[e[1]].append(e[0])
        except: vertex[e[1]] = [e[0]]
    print(vertex)
solution(6, [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]])      

{3: [6, 4, 2, 1], 6: [3], 4: [3, 2], 2: [3, 1, 4, 5], 1: [3, 2], 5: [2]}

다익스트라 알고리즘을 사용하기 위해 방문 배열과 거리비용 배열을 생성 합니다. 그리고 첫번째 노드를 0으로 설정 합니다.

def solution(N, edge):
    vertex = {}
    for e in edge:
        try: vertex[e[0]].append(e[1])
        except: vertex[e[0]] = [e[1]]
        try: vertex[e[1]].append(e[0])
        except: vertex[e[1]] = [e[0]]
            
    visited = [False for _ in range(N)]   # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]   # 거리비용 배열 선언
    cost[0] = 0   # 출발할 노드의 값을 0으로 설정
    
    print(visited)
    print(cost)
    
solution(6, [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]])      

[False, False, False, False, False, False]
[0, 2147483647, 2147483647, 2147483647, 2147483647, 2147483647]

다음 노드 탐색을 위해서 BFS를 이용합니다. deque() 리스트 checkNode를 생성하여 너비 우선 탐색을 수행 합니다. 리스트의 첫번째 값은 첫 노드의 값 1을 넣어줍니다.

    checkNode = deque()  # 노드 탐색을 위한 queue 리스트
    checkNode.append(1)

checkNode 리스트에 값이 없을 때 까지 루프를 지속 하며 가장 먼저넣어준 노드의 값을 빼고 해당 노드의 방문 배열을 True로 변경 합니다.

    while checkNode:
        now = checkNode.popleft()
        visited[now-1] = True

해당 노드와 연결된 다른 노드를 vertex 딕셔너리를 통해 찾고 연결된 노드 중 방문하지 않았고(방문 배열이 False) 탐색 리스트 checkNode에 등록되지 않은 노드를 검색합니다.

        for node in vertex[now]:
            if visited[node-1] == False and node not in checkNode:

탐색한 노드의 cost 값은 기존 값과 현재 검색하고 있는 now 노드에 길이 값(1)을 더한 값 중 작은 값이 해당 노드의 최소 비용이 됩니다. 위 내용의 코드는 아래와 같습니다.

from collections import deque

def solution(N, edge):
    vertex = {}
    for e in edge:
        try: vertex[e[0]].append(e[1])
        except: vertex[e[0]] = [e[1]]
        try: vertex[e[1]].append(e[0])
        except: vertex[e[1]] = [e[0]]

    visited = [False for _ in range(N)]   # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]   # 거리비용 배열 선언
    cost[0] = 0   # 출발할 노드의 값을 0으로 설정

    checkNode = deque()  # 노드 탐색을 위한 queue 리스트
    checkNode.append(1)
    while checkNode:
        now = checkNode.popleft()
        visited[now-1] = True
        for node in vertex[now]:
            if visited[node-1] == False and node not in checkNode:
                cost[node-1] = min(cost[node-1], cost[now-1] + 1)
                checkNode.append(node)
    print(cost)

solution(6, [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]])

[0, 1, 1, 2, 2, 2]

마지막으로 거리비용 배열(cost list)을 정렬 후 가장 큰 값에 동일한 값의 수를 계산 합니다.

from collections import deque

def solution(N, edge):
    vertex = {}
    for e in edge:
        try: vertex[e[0]].append(e[1])
        except: vertex[e[0]] = [e[1]]
        try: vertex[e[1]].append(e[0])
        except: vertex[e[1]] = [e[0]]

    visited = [False for _ in range(N)]   # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]   # 거리비용 배열 선언
    cost[0] = 0   # 출발할 노드의 값을 0으로 설정

    checkNode = deque()  # 노드 탐색을 위한 queue 리스트
    checkNode.append(1)
    while checkNode:
        now = checkNode.popleft()
        visited[now-1] = True
        for node in vertex[now]:
            if visited[node-1] == False and node not in checkNode:
                cost[node-1] = min(cost[node-1], cost[now-1] + 1)
                checkNode.append(node)
    cost.sort()
    return sum(cost[-1] == c for c in cost)

print(solution(6, [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]))

3

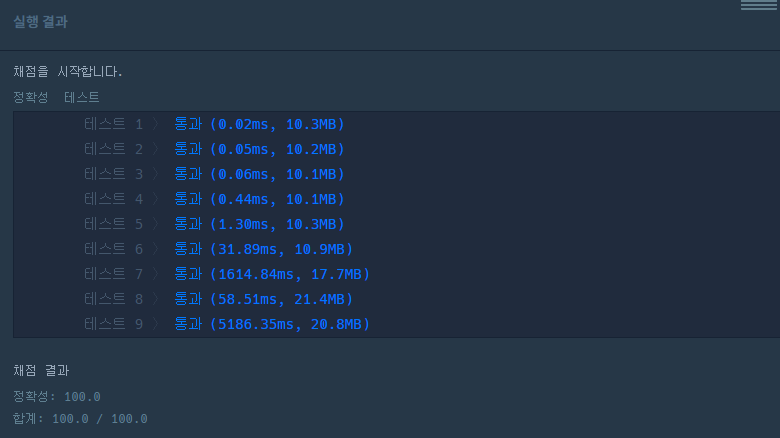
결과는 아래와 같이 잘 통과 되는 것을 확인 할 수 있습니다.