프로그래머스 - 배달 (다익스트라)

이번 포스팅에서는 프로그래머스의 배달 (다익스트라) 코딩테스트 연습 문제를 풀어봅니다.

문제 설명

N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

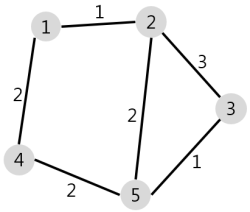
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.

제한사항

• 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
• road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
• road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
• road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
  • a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
  • 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
  • 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
• K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
• 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
• 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.

입출력 예

N	road	K	result
5	[[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]]	3	4
6	[[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]]	4	4

입출력 예 설명

입출력 예 #1
문제의 예시와 같습니다.

입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

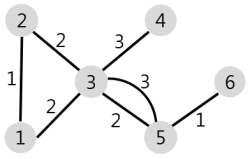
1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.

문제 풀이

다른 노드까지의 최단 경로를 구하는 다익스트라 알고리즘을 사용 하여 문제를 해결 합니다.

먼저 방문 배열과 비용&거리 배열을 선언 하고 1번 마을로 설정할 0번 노드를 시작점으로 설정 하여 거리 비용을 0으로 합니다.

def solution(N, road, K):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    visited[0] = False  # 0 번 노드를 시작점으로 설정
    cost[0] = 0
    print(visited)
    print(cost)

solution(5, [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]], 3)

[False, False, False, False, False]
[0, 2147483647, 2147483647, 2147483647, 2147483647]

방문 배열이 모두 True가 될때 까지 루프를 지속합니다. 먼저 방문하지 않은 지역 중 최솟값을 찾고 더이상 검사할 후보가 없다면 루프를 종료 합니다.

def solution(N, road, K):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    visited[0] = False  # 0 번 노드를 시작점으로 설정
    cost[0] = 0
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        # 방문하지 않은 지역 중 최솟값 찾기
        checkLoc = -1
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break

solution(5, [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]], 3)

검사할 대상의 방문 배열을 True로 변경하고 road 리스트의 값을 통해 경로 완전탐생을 수행하고 비용 배열의 값을 수정합니다.
루프가 모두 완료 되면 마을 1에서 각 마을 까지의 최단 경로 시간을 얻을 수 있습니다.

def solution(N, road, K):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    visited[0] = False  # 0 번 노드를 시작점으로 설정
    cost[0] = 0
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        # 방문하지 않은 지역 중 최솟값 찾기
        checkLoc = -1
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break
        visited[checkLoc] = True # 검사할 대상의 방문 배열을 True로 변경
        for v1, v2, c in road:  # 경로 완전탐색으로 비용배열 수정
            v1 -= 1 # 방문 및 비용 배열은 0부터 시작 함으로 마을 번호를 -1씩 빼고 계산
            v2 -= 1
            if v1 == checkLoc and visited[v2] == False: # 검사할 대상과 road배열의 값과 일치 하고 연결된 마을이 방문한 노드가 아니라면
                cost[v2] = min(cost[v2], cost[v1] + c)  # 연결된 마을의 거리 비용 값을 두개의 값(기존 값, 검사할 대상의 거리 비용 값과 거리 시간 값)을 비교한 값 중 작은 값으로 변경
            if v2 == checkLoc and visited[v1] == False: # road배열은 양방향 정보이기에 반대 방향도 확인
                cost[v1] = min(cost[v1], cost[v2] + c)
    print(cost)

solution(5, [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]], 3)

[0, 1, 4, 2, 3]

마지막으로 거리 비용 배열에서 K 시간 이하의 총 갯수를 반환 합니다.
예제 입력을 추가하여 확인 해 보았습니다.

def solution(N, road, K):
    visited = [False for _ in range(N)]  # 방문 배열 선언
    cost = [2**31-1 for _ in range(N)]  # 비용 배열, 거리 배열 선언
    visited[0] = False  # 0 번 노드를 시작점으로 설정
    cost[0] = 0
    length = len(visited)
    while False in visited:  # 방문하지 않은 노드가 있다면 루프를 지속함
        # 방문하지 않은 지역 중 최솟값 찾기
        checkLoc = -1
        checkValue = 2**31-1
        for i in range(length):
            if visited[i] == False and cost[i] < checkValue: # 방문 배열이 False인 값 중 비용 배열이 최소인 값
                checkLoc = i
                checkValue = cost[i]
        if checkLoc == -1:  # 검사할 후보가 없다면 탈출
            break
        visited[checkLoc] = True # 검사할 대상의 방문 배열을 True로 변경
        for v1, v2, c in road:  # 경로 완전탐색으로 비용배열 수정
            v1 -= 1 # 방문 및 비용 배열은 0부터 시작 함으로 마을 번호를 -1씩 빼고 계산
            v2 -= 1
            if v1 == checkLoc and visited[v2] == False: # 검사할 대상과 road배열의 값과 일치 하고 연결된 마을이 방문한 노드가 아니라면
                cost[v2] = min(cost[v2], cost[v1] + c)  # 연결된 마을의 거리 비용 값을 두개의 값(기존 값, 검사할 대상의 거리 비용 값과 거리 시간 값)을 비교한 값 중 작은 값으로 변경
            if v2 == checkLoc and visited[v1] == False: # road배열은 양방향 정보이기에 반대 방향도 확인
                cost[v1] = min(cost[v1], cost[v2] + c)

    return sum(K >= c for c in cost) # 거리 비용 배열에서 K 시간 이하의 총 갯수를 반환

print(solution(5, [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]], 3))
print(solution(6, [[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]], 4))

4
4

결과는 아래와 같이 잘 통과 되는 것을 확인 할 수 있습니다.