연결리스트 / 트라이구조

August 30, 2021 5 분 소요

이번 포스팅은 자료구조의 연결리스트와 트라이구조에 대해서 정리해보겠습니다.

1. 연결리스트

연결리스트(LinkedList) 란?

각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 데이터를 저장하는 자료 구조 입니다.

아래와 같이 5, 7, 10 성분을 가지고 있는 리스트가 있을때 리스트는 인덱스를 활용하여 값을 저장하는 반면, 앞에 있는 값이 바로 뒤에 있는 성분을 기억 또는 연결하는 구조를 가지고 있습니다.

연결리스트와 리스트

아래와 같이 [A, B, C, E, F, G] 라는 리스트에 D라는 값을 C와 E 사이에 넣을때 E, F, G의 인덱스를 재조정해야 합니다.

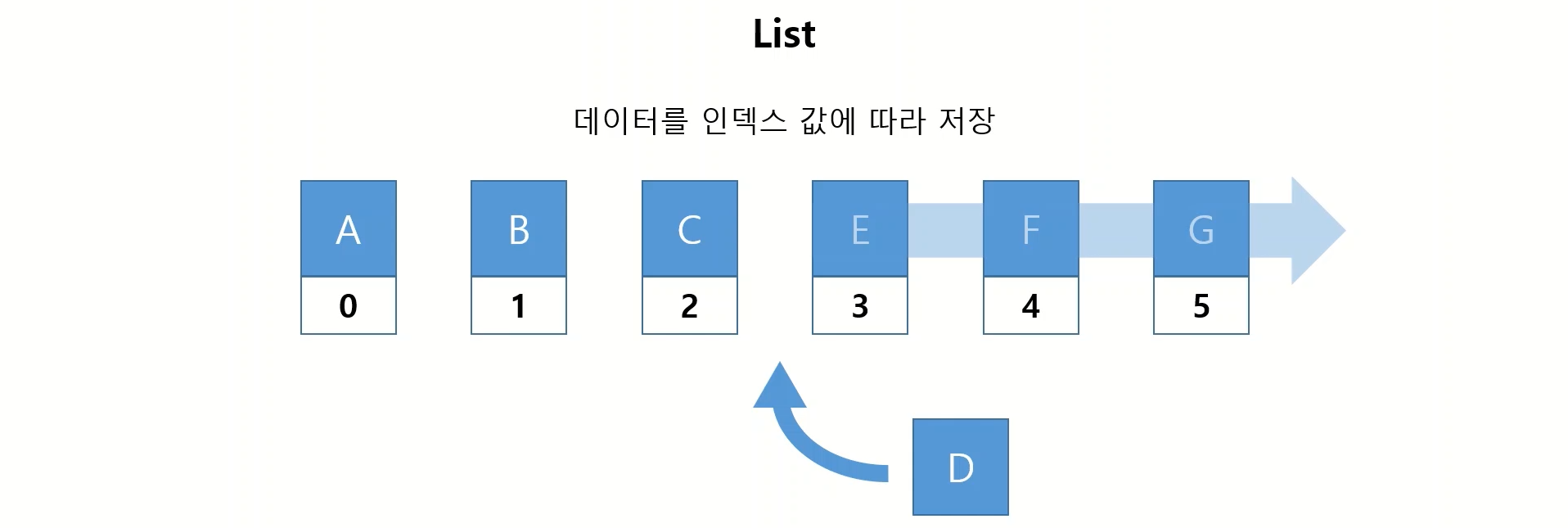
또한 반대로 리스트의 중간에서 삭제를 하게 된다면 뒤에있는 성분의 인덱스를 재조정해야 합니다.

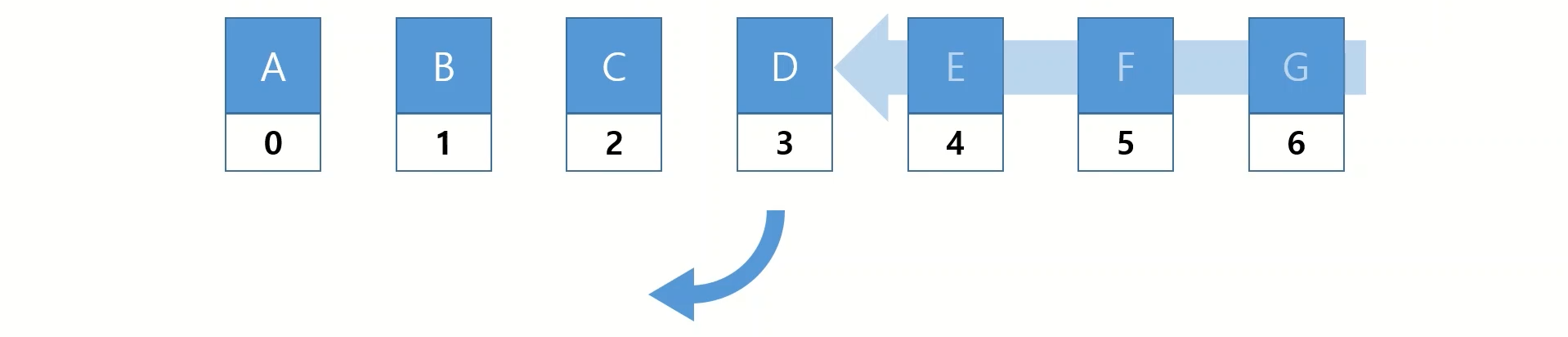
이는 대량의 데이터에서 추가와 삭제 시 성능이 저하되는 원인이 됩니다.
—

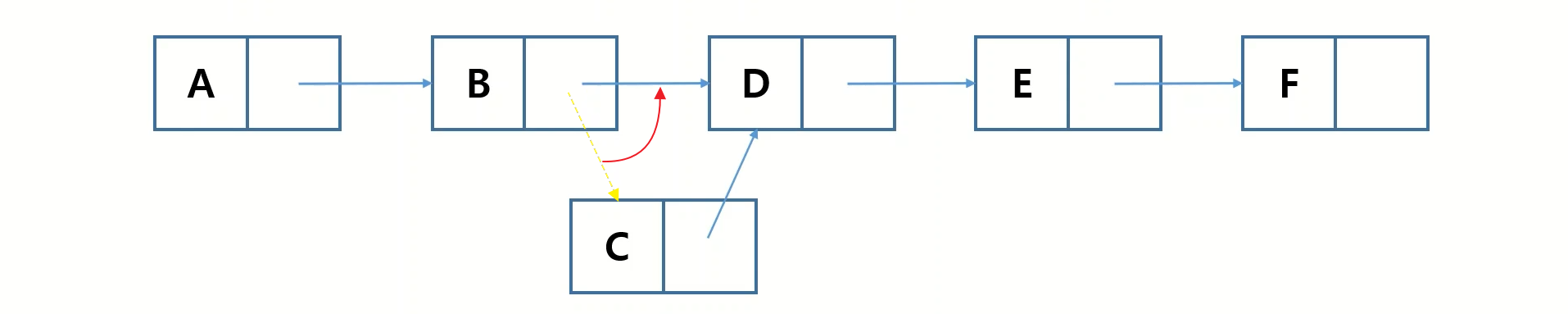
리스트와 마찬가지로 연결 리스트에 C라는 값을 B와 D사이에 넣을때 연결 리스트 에서는 단지 B와 D의 연결을 끊고 B->C->C로 연결해 주면 됩니다.

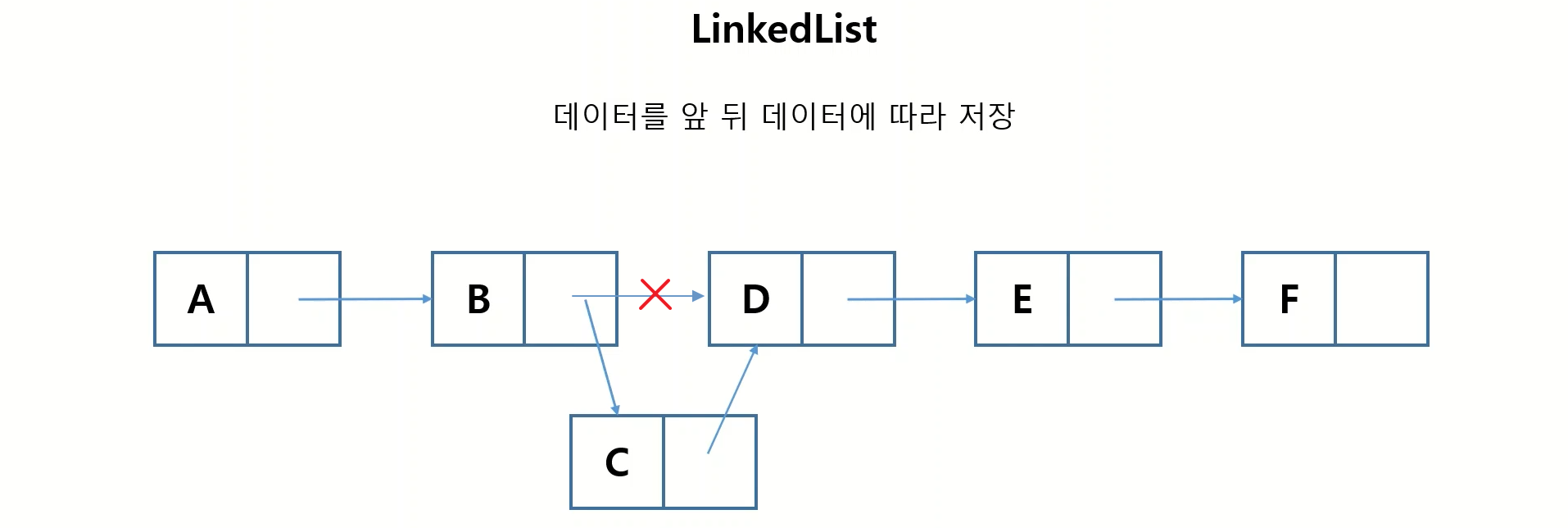
또한 반대로 연결 리스트의 중간에서 삭제를 하게 된다면 삭제할 노드의 앞의 노드를 다음 노드로 연결해 주기만 하면 됩니다.

연결리스트 구현

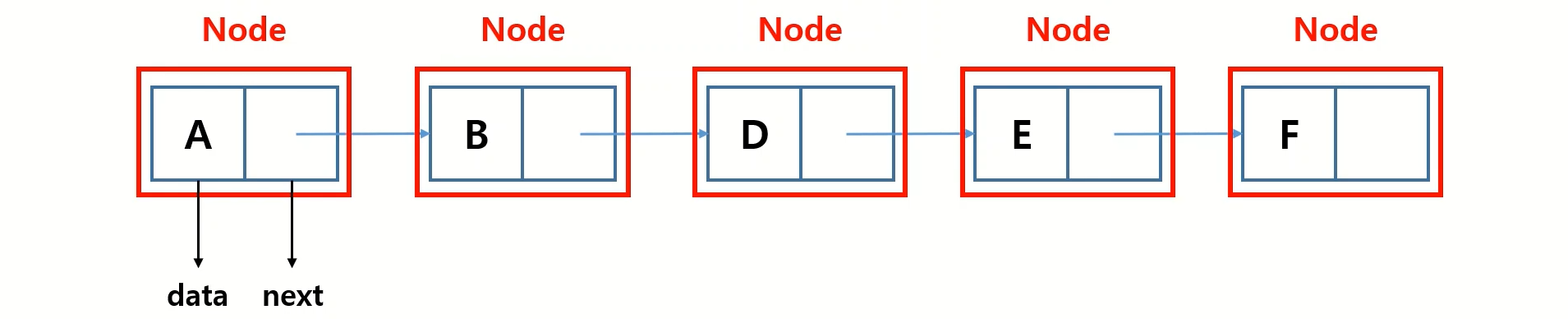
연결 리스트는 각 요소인 노드를 연결하는 구조로 되어 있고 하나의 노드는 데이터를 담는 data 파트와 다음 노드를 담는 next 파트로 이루어져 있습니다.

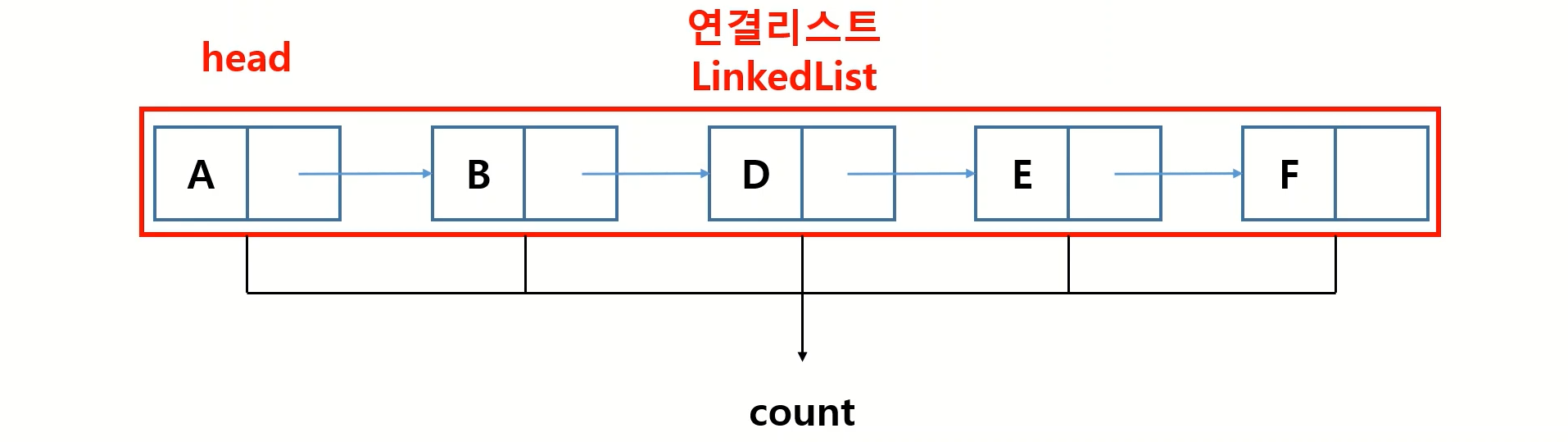
그리고 부가적으로 첫번째 노드를 표시해줄 head와 총 노드의 수를 표현할 count를 구성 할 수 있습니다.

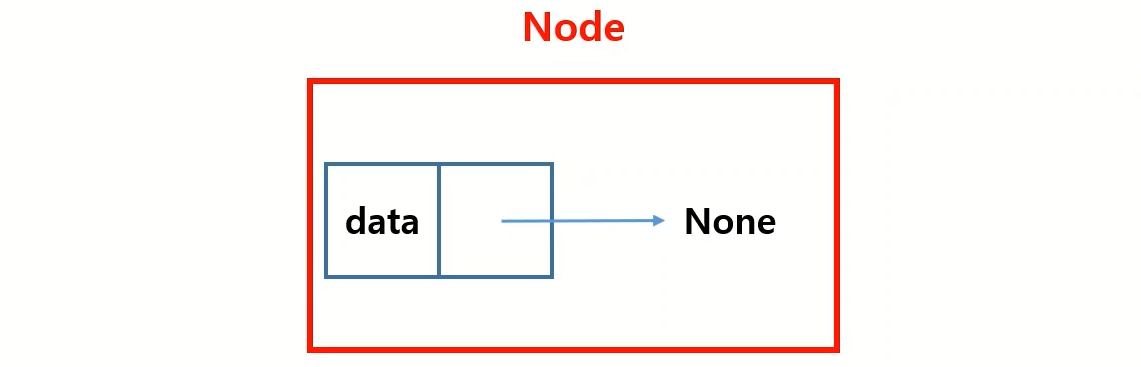
노드

연결 리스트의 요소인 노드를 구성 합니다. 데이터를 담는 data 파트와 다음 노드를 담는 next 파트를 초기화 합니다.

class Node():
    def __init__(self, data):
        self.data = data
        self.next = None

연결리스트

연결 리스트 객체를 생성할 때는 고유한 데이터가 없을 것 임으로 다음과 같이 생겼을 것 입니다. 코드로 구성 하면 아래와 같습니다.

class LinkedList():
    def __init__(self):
        self.head = None
        self.count = 0

맨 앞에 데이터를 새롭게 추가하는 함수입니다. head에 데이터가 없을때 즉 아무 데이터가 없을때와 비어있지 않을때를 구성 할 수있습니다.

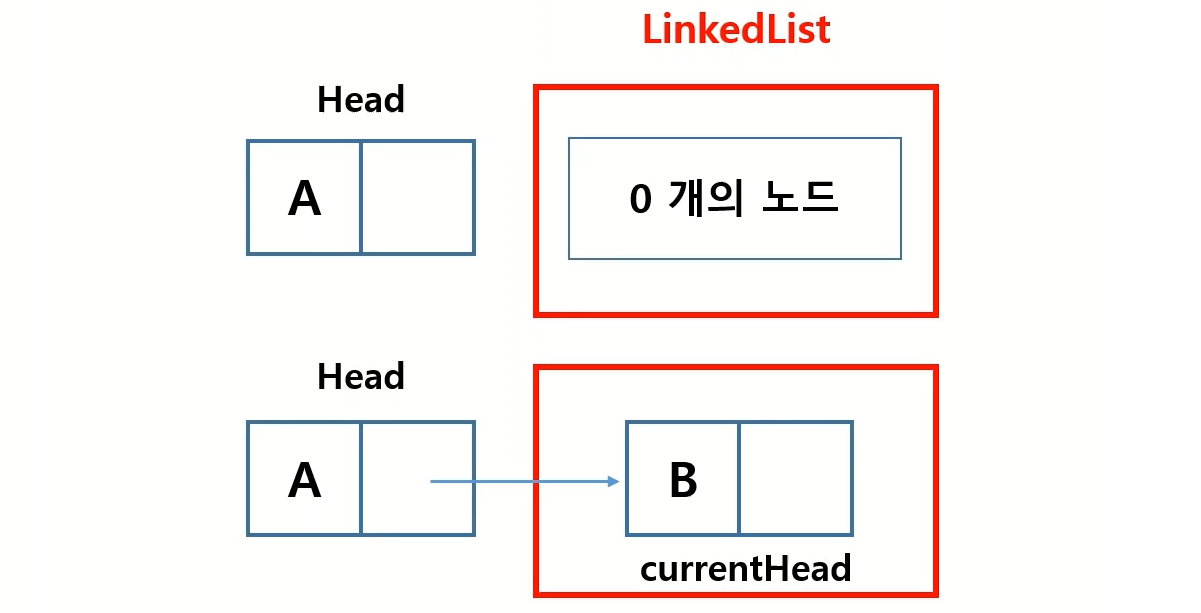
    def appendHead(self, node): 
        if self.head == None: # 만약 head가 없다면 연결 리스트에 아무 데이터가 없을때
            self.head = node # head는 새로 생성된 노드를 가지게 됨
            self.count = 1
        else: # 만약 연결 리스트가 비어 있지 않다면
            self.count += 1
            currentHead = self.head # 기존의 노드를 현재 헤드로 저장
            self.head = node # 헤드에 새롭게 추가한 노드 저장
            node.next = currentHead # 새롭게 추가한 노드의 연결 노드에 기존의 노드 추가

연결리스트 마지막에 데이터를 추가하는 함수입니다.

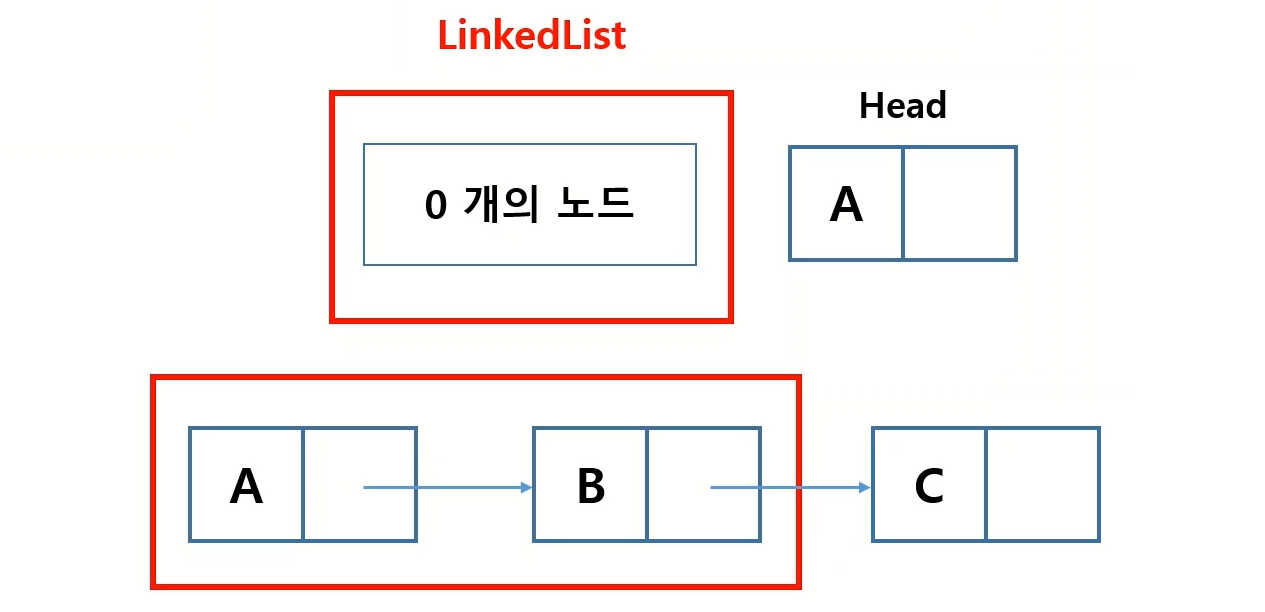
    def append(self,node):
        if self.head == None: # 만약 head가 없다면 연결 리스트에 아무 데이터가 없을때
            self.head = node # head는 새로 생성된 노드를 가지게 됨
            self.count = 1
        else:   # 만약 연결 리스트가 비어 있지 않다면
            now = self.head
            while now.next != None:  #연결리스트가 끝에 도달할 때까지
                now = now.next
            now.next = node  # 맨 끝 노드의 연결 노드에 새롭게 등록한 노드 추가
            self.count += 1

특정 위치에 데이터를 추가하는 함수입니다.

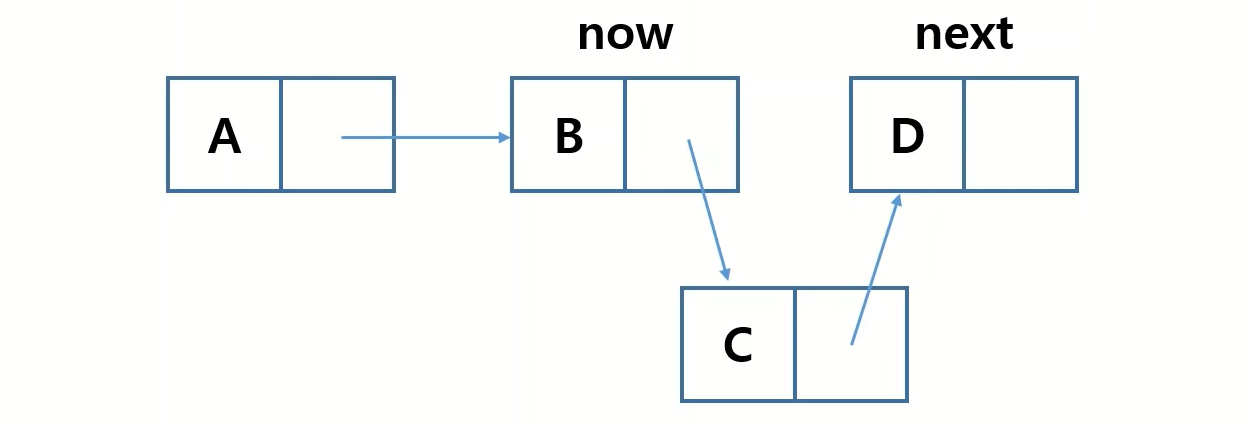
    def insertNodeAtIndex(self, node, index):  # 데이터를 보유한 노드, 넣을 위치의 숫자
        if index < 0 or index > self.count:  # 노드의 범위를 벗어 났을때는 작업을 종료
            return -1
        elif self.count == index:  # 인덱스의 값과 보유한 노드의 숫자가 같다면 => 연결 리스트의 마지막에 데이터를 추가하는 작업
            self.append(node)  # 앞서 작성한 append() 함수의 작업과 동일
        elif indeex == 0:  # 인덱스 값이 0이면 => 연결 리스트의 맨 앞에 데이터를 추가하는 작업
            self.appendHead(node)  # 앞서 작성한 appendHead() 함수의 작업과 동일
        else:   # 위의 작업이 모두 아니면 중간에 삽입 하는 경우
            now = self.head
            while index > 0:  # 현재의 위치가 데이터를 담기 원하는 위치 까지 이동
                index -= 1
                now = now.next
            self.count += 1
            next = now.next  # 현재 위치의 다음 노드 값을 임시 저장
            now.next = node  # 현재 위치의 다음 노드 값을 새로 추가한 노드로 변경
            node.next = next  # 새로 추가한 노드의 다음 노드를 next 변수에 임시 저장한 노드를 입력

다음은 데이터를 삭제하는 함수 입니다. 먼저 헤드의 위치에 지우길 원하는 데이터가 있을때 입니다.

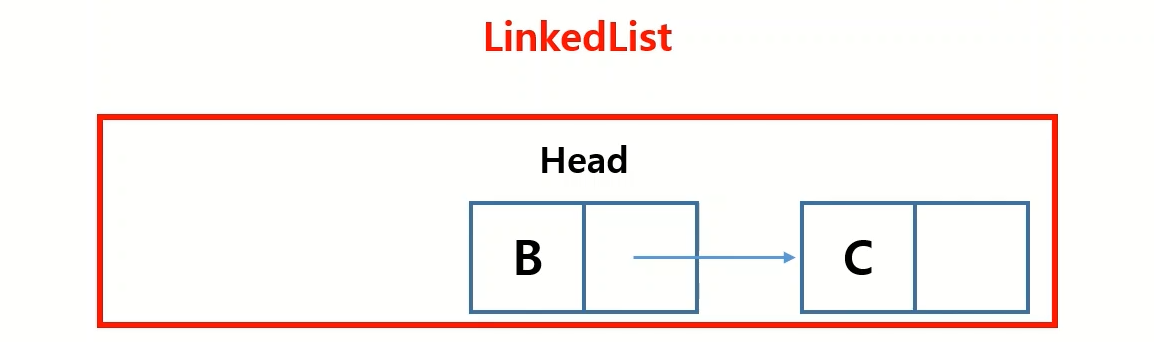
    def deleteData(self, data):
        if self.head.data == data:   # 현재 헤드의 데이터가 지우길 원하는 데이터 라면
            self.head = self.head.next   # 헤드의 다음 노드를 현재 헤드로 지정
            self.count -= 1

만약 원하는 데이터가 헤드에 위치하지 않다면 원하는 데이터가 나올때 까지 찾아 내려가야 합니다.

        else:
            first = self.head  # 현재 헤드
            second = first.next   # 현재 헤드의 다음 노드
            while second != Node:  # 원하는 데이터가 나올때 까지 노드의 끝까지 탐색
                if second.data == data:  # second의 데이터가 원하는 데이터 값이면
                    first.next = second.next  # fist의 다음 노드를 second의 다음 노드로 설정(second 노드 제거)
                    self.count -= 1
                    break
                first = second    # 만약 second 데이터가 조건에 일치 하지 않으면 노드의 자리를 하나씩 이동
                second = second.next  

마지막으로 연결 리스트의 데이터가 몇개의 데이터가 있는지를 알아보는 함수는 count 변수를 반환 합니다.

    def getCount(self):
        return self.count

2. 트라이구조

트라이(Trie)구조란?

문자열을 효율적으로 저장하고 탐색하기 위한 트리 형태의 자료구조 입니다.

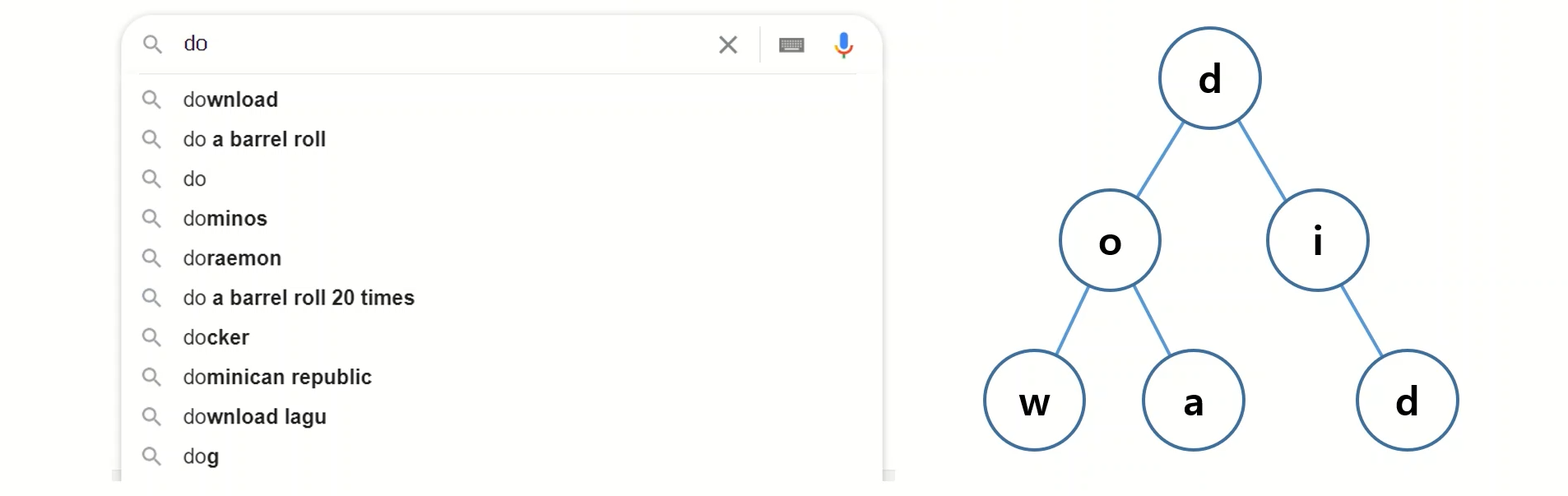
아래에 보이는 트리의 루트에서부터 자식들을 따라가면서 생성된 문자열들이 트라이 자료구조에 저장되어 있다고 볼 수 있습니다.

DFS 형태로 검색을 해보면 DOG, DOT, DID 라는 단어들이 자료구조에 들어가 있음을 알 수 있습니다.

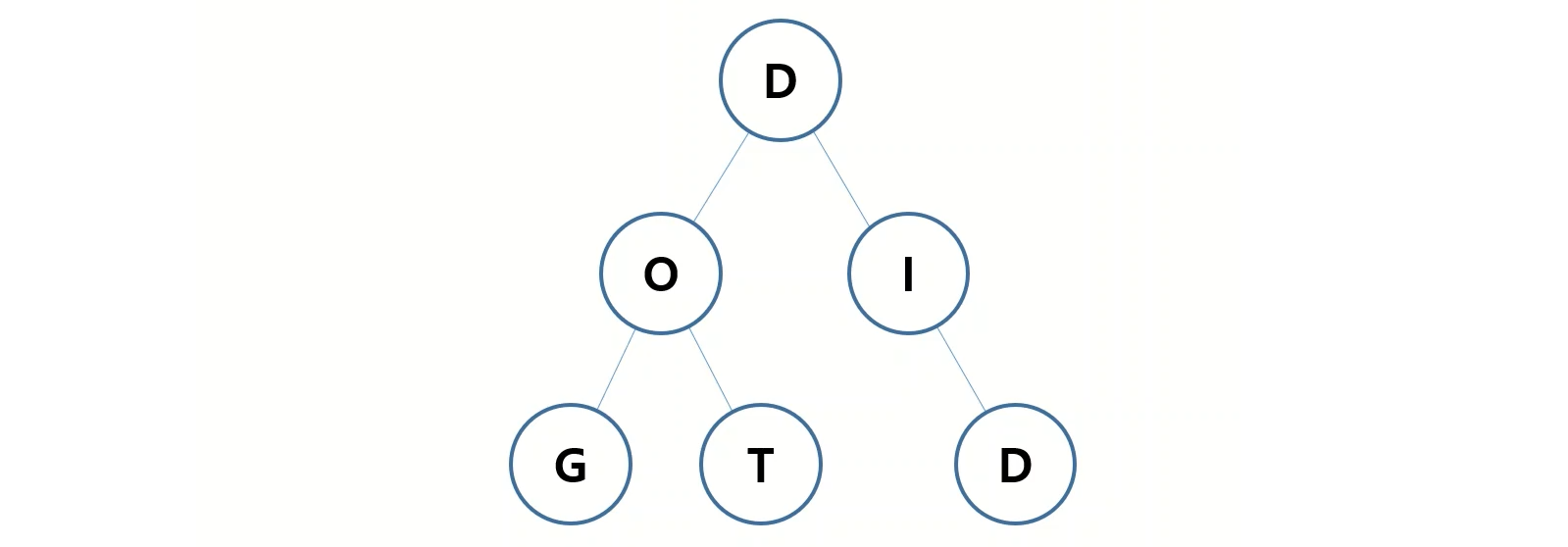
트라이(Trie)구조 구현

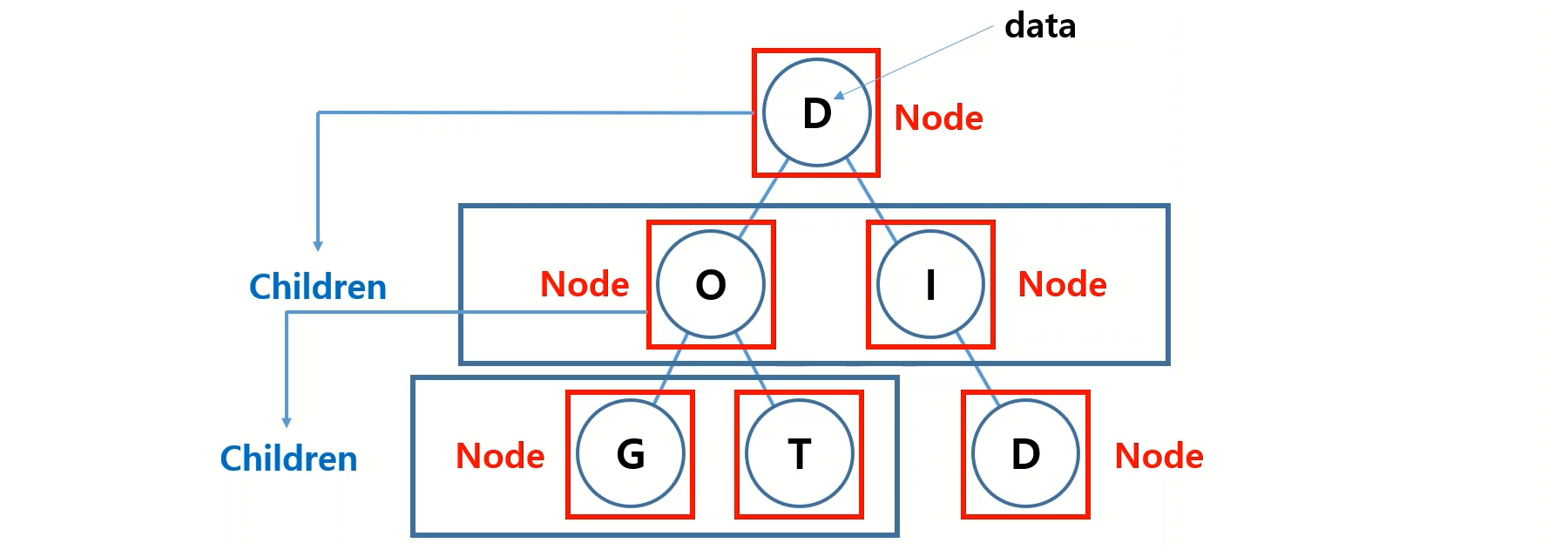
먼저 연결 리스트 처럼 노드가 존재 하고 각 노드는 data와 아래 하위 자식 노드들을 가지고 있습니다. 이러한 노드들은 반복해서 자식 노드들을 갖게 되는 구조 입니다.

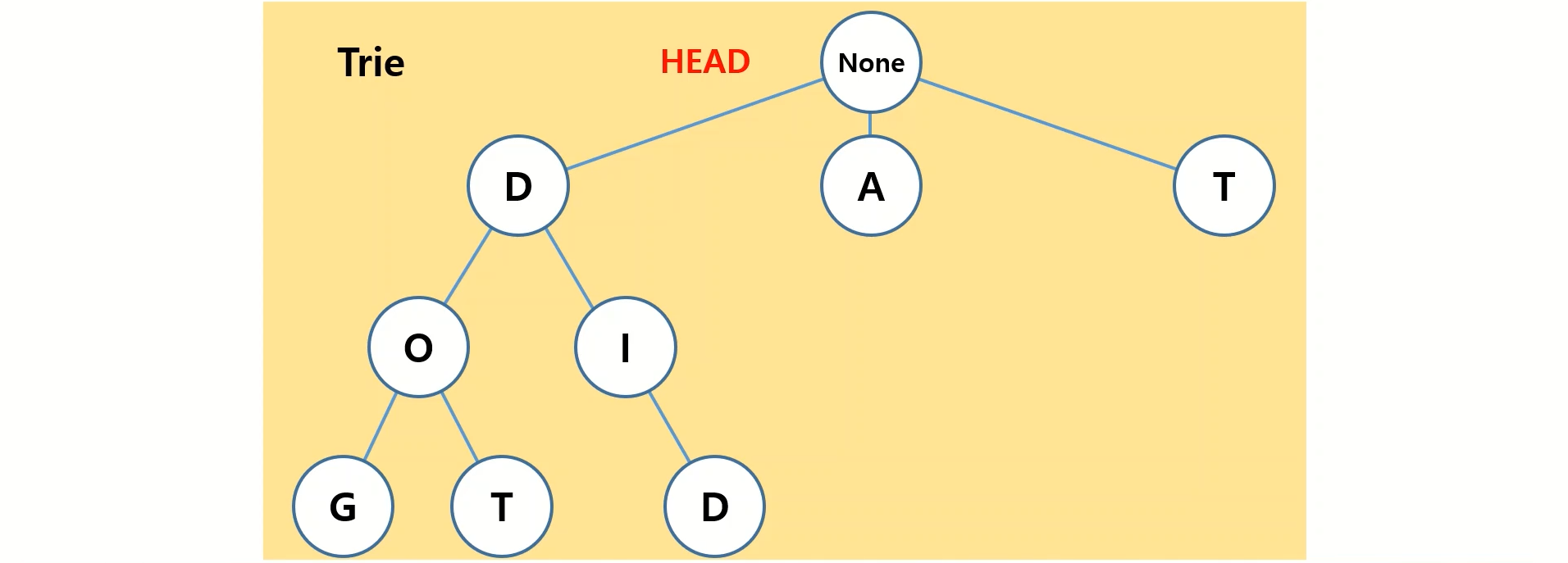
트라이 구조의 전체적인 구조입니다. 문자열은 D에서부터만 시작하는 것이 아니기에 트라이 구조의 최상위 노드는 None 을 가지게 되고 None 값의 자식 노드 부터 원하는 문자열을 시작 할 수 있어야 합니다. 이때 None 값을 가진 최상위 노드를 head라 합니다.

노드

트라이 구조의 노드 클래스를 먼저 구현해 보겠습니다. 트라이 구조는 data와 자식 노드를 가지게 될 리스트 또느 헤시를 가짐으로 아래와 같이 생성 합니다.

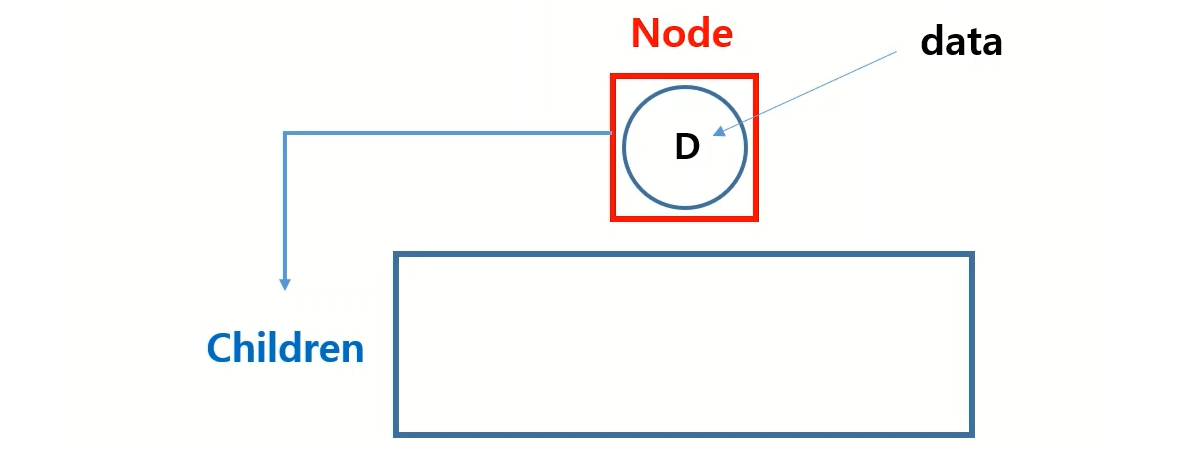
class Node():
    def __init__(self, data):
        self.data = data
        self.children = {}

트라이(Trie) 구조

트라이 구조의 최상위 노드는 None값을 가짐으로 아래와 같이 head를 생성 합니다.

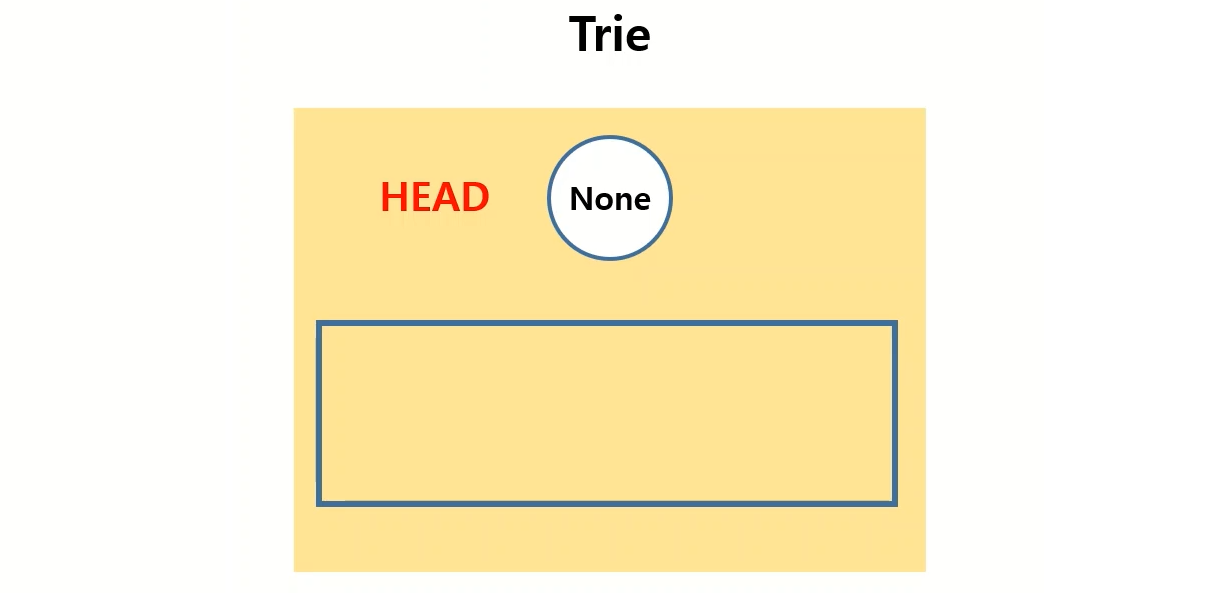
class Trie():
    def __init__(self, data):
        self.head = Node(None)

트라이 구조의 데이터를 삽입하는 함수 입니다.

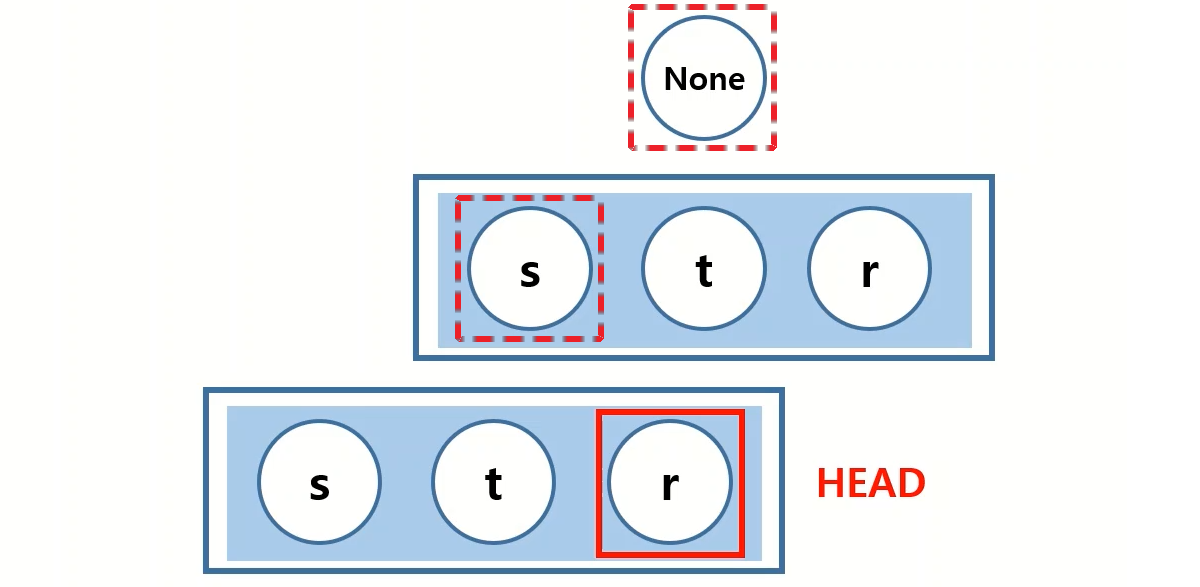
    def insert(self, string):
        head = self.head   # 트라이 구조의 최상위 부모를 호출
        for s in string:   # 트라이 구조에 넣기 원하는 문자열을 반복문을 이용하여 한글자씩 읽음
            children = head.children  # 현재 최상위 부모의 자식 노드를 불러오고
            if s not in children:   # 자식 노드 안에 현재 넣길 원하는 첫번째 문자의 존재 여부를 확인
                children[s] = Node(s)   # 만일 원하는 글자가 없다면 자식 노드에 새로운 노드를 추가
            head = children[s]   # 추가된 자식을 다시 헤드로 지정하여 다음 문자열에 대한 작업을 반복
            #  ※ 만약 자식 노드 중에 다음 문자열이 있다면 바로 다음 문자열의 노드를 새로운 부모로 지정 하게 됨

트라이(Trie) 구조 활용

트라이 구조의 대표적인 활용 예는 추천 검색어가 있습니다. 한글자 한글자를 입력 할때 마다 각각의 단어들이 이전의 사용자가 몇번을 검색 했는지 검색 횟수를 가지고 있고 그에 맞추어 가장 많이 사용된 다음 문자열을 추천해 주는 방식을 활용 할 수 있습니다.

Twitter Facebook LinkedIn

ParkYongYeon