최단경로 탐색법

이번 포스팅은 자료구조의 최단경로 탐색법을 정리해보겠습니다.

최단경로

최단경로 알고리즘

출발지부터 도착지까지 최단거리 혹은 최소 비용을 지불 함으로서 도착하는 것이 그 목적 입니다.

최단경로 알고리즘 유형

• 플로이드 와샬 알고리즘 : 모든 노드를 방문하는 최단 경로
• 다익스트라 알고리즘 : 특정 노드에서 다른 노드까지의 최단 경로

1. 플로이드 와샬 알고리즘

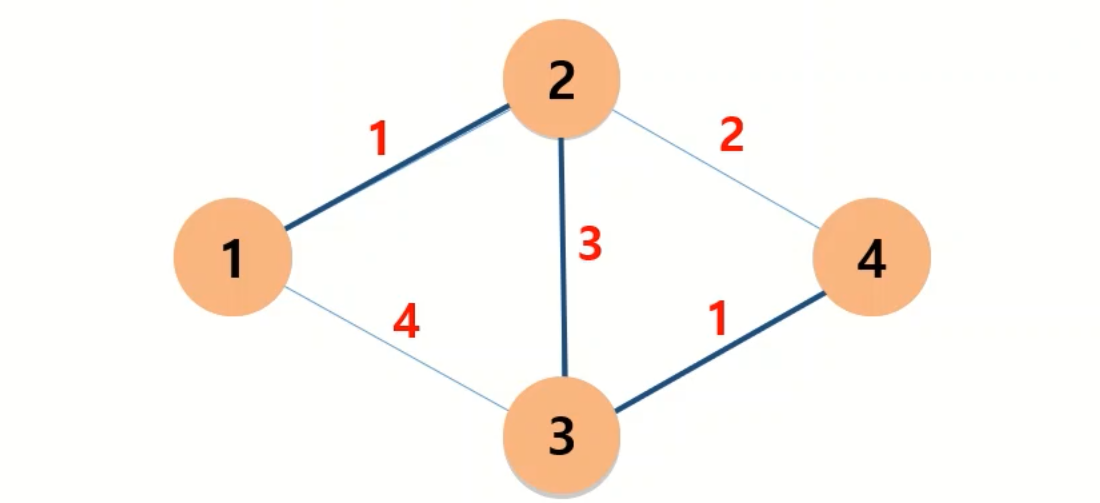
주어진 것 처럼 노드와 경로가 있을 때 모든 노드를 최소비용 혹은 최단 경로로 연결하는 알고리즘 입니다.

플로이드 와샬 구현방법

모든 노드를 방문하는 최단 경로를 구하는 플로이드 와샬의 구현 방법은 아래와 같은 과정을 가집니다.

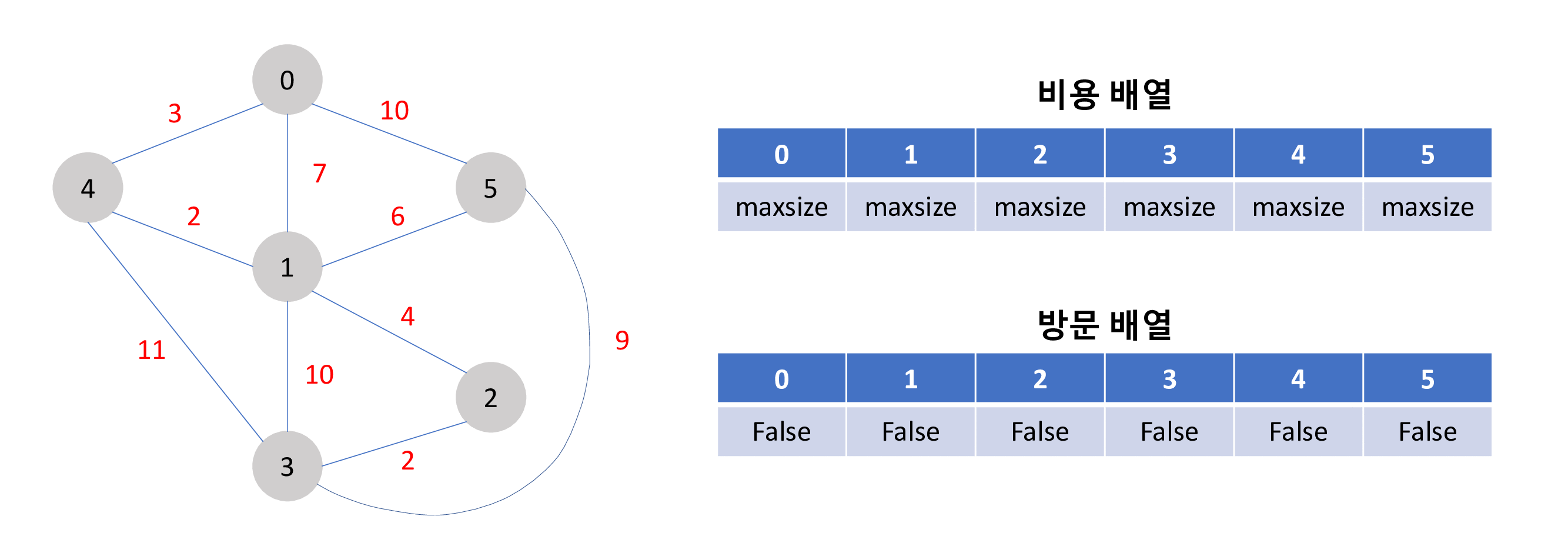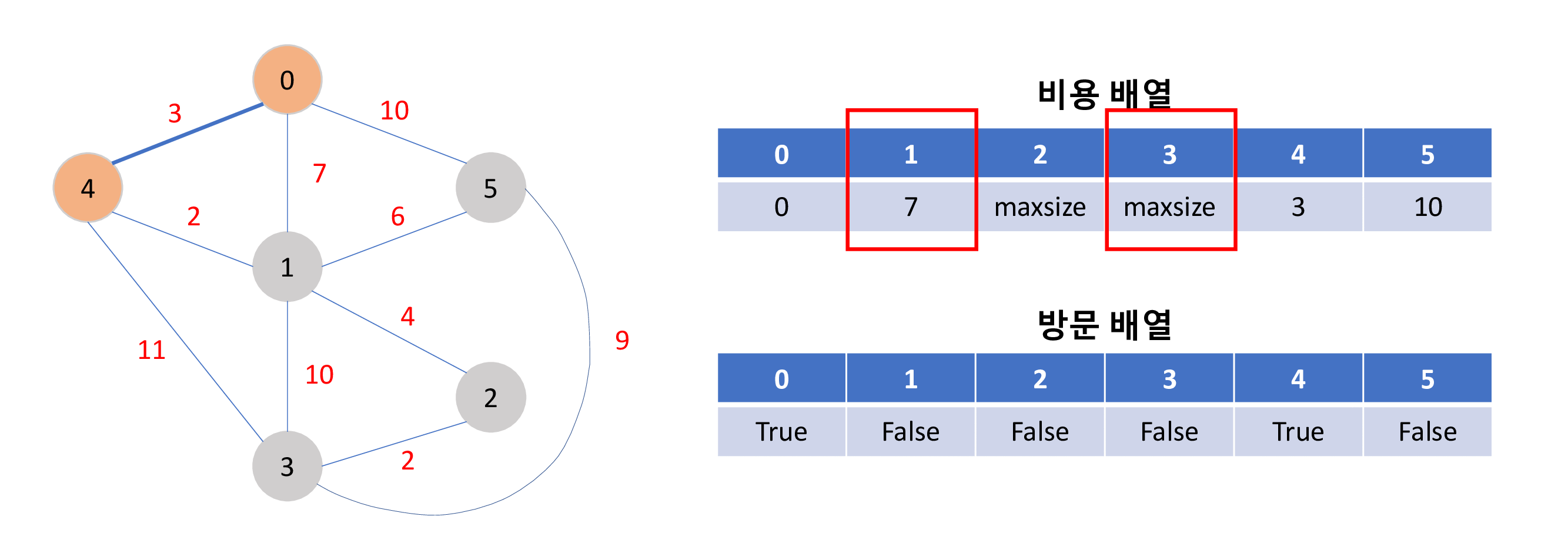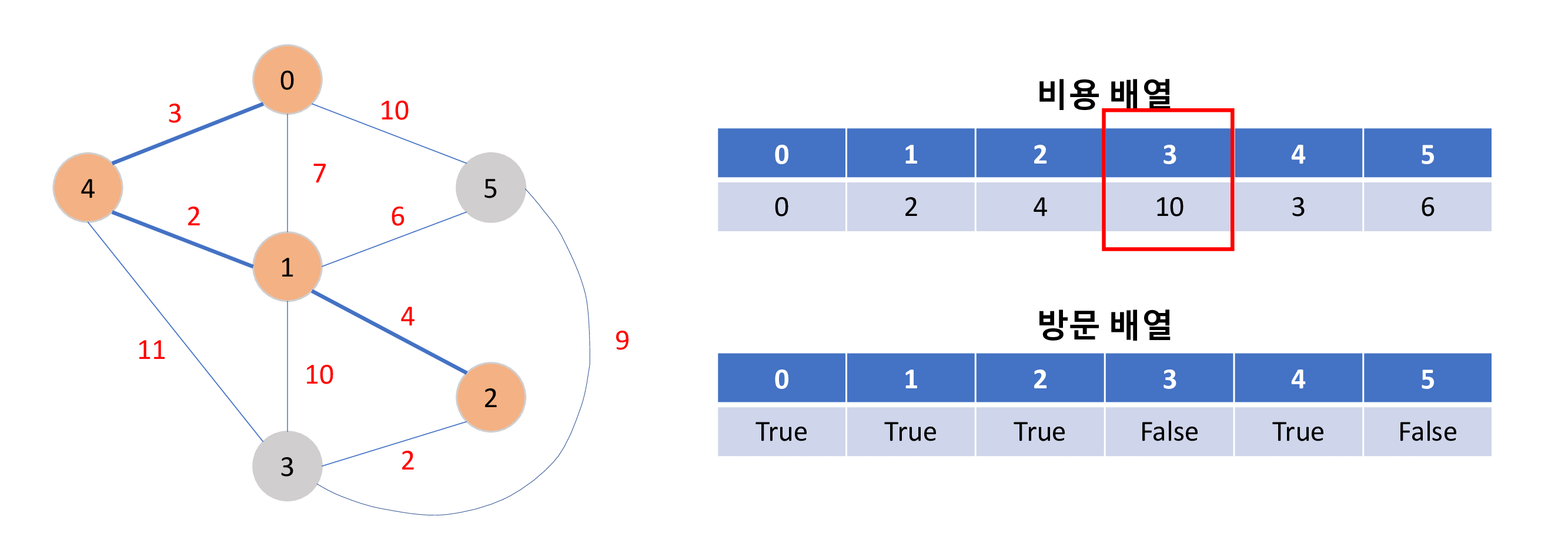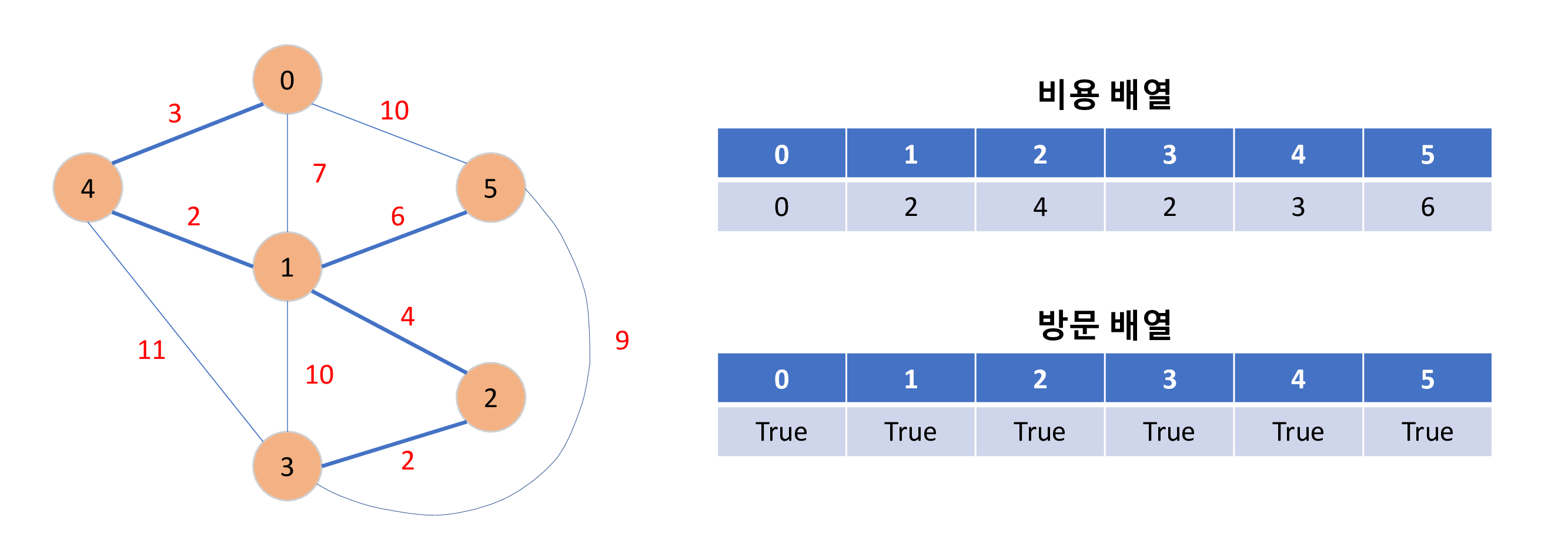
비용 배열과 방문 배열을 이용하여 방문 배열이 모두 True일때 비용 배열의 합 0 + 2 + 4 + 2 + 3 + 6 = 17 이 최소비용 입니다.

플로이드 와샬 예시코드

플로이드 와샬을 구현 하는 예시코드는 아래와 같습니다.

values = [2**31-1 for i in range(n)] # 비용 배열, 거리 배열 선언 (2**31-1 => 정수 자료형 최대 범위)
visited = [False for i in range(n)] # 방문 배열 선언
start = 0     # 0번 노드를 시작점으로 설정
visited[start] = True    # 첫 방문 노드 
values[start] = 0
while False in visited:  # 방문하지 않은 노드가 있다면
    for i in costs:       # 노드 완전탐색으로 비용배열의 거리 값 최소화
        if(visited[i[0]]==False and i[0]==start):
            values[i[0]] = min(values[i[1]], i[2])
        if(visited[i[0]]==False and i[1]==start):
            values[i[0]] = min(values[i[0]], i[2])
    refer = 2**31-1
    for i in range(n):    # 방문하지 않은 노드 중 최소 비용 노드 위치 탐색
        if(visited[i]==False and values[i]!=0):
            refer = min(refer, values[i])
    answer = answer + refer
    for i in range(n):    # 해당 노드 방문 여부 체크
        if(visited[i]==False and values[i]==refer):
            visited[i] = True
            start = i
            break

2. 다익스트라 알고리즘

특정노드에서 특정노드까지의 경로를 찾을때 최단거리를 찾는 알고리즘 입니다.
그림에서 1번 노드 -> 4번 노드의 경로를 찾을때 최단 경로는 다음과 같습니다.

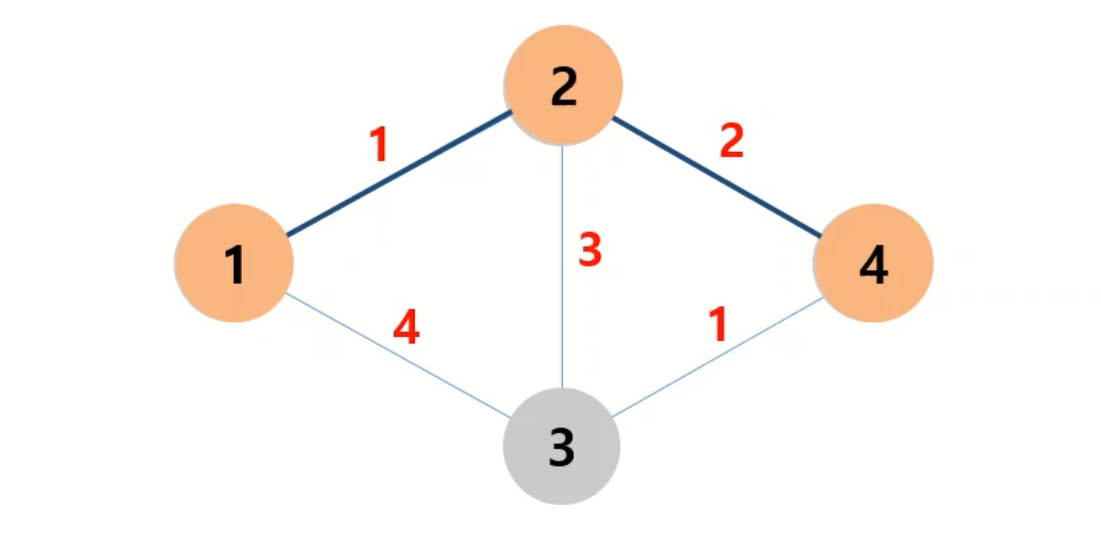
다익스트라 구현방법

특정 노드에서 다른 노드까지의 최단 경로를 구하는 다익스트라 알고리즘 구현 방법은 아래와 같은 과정을 가집니다.

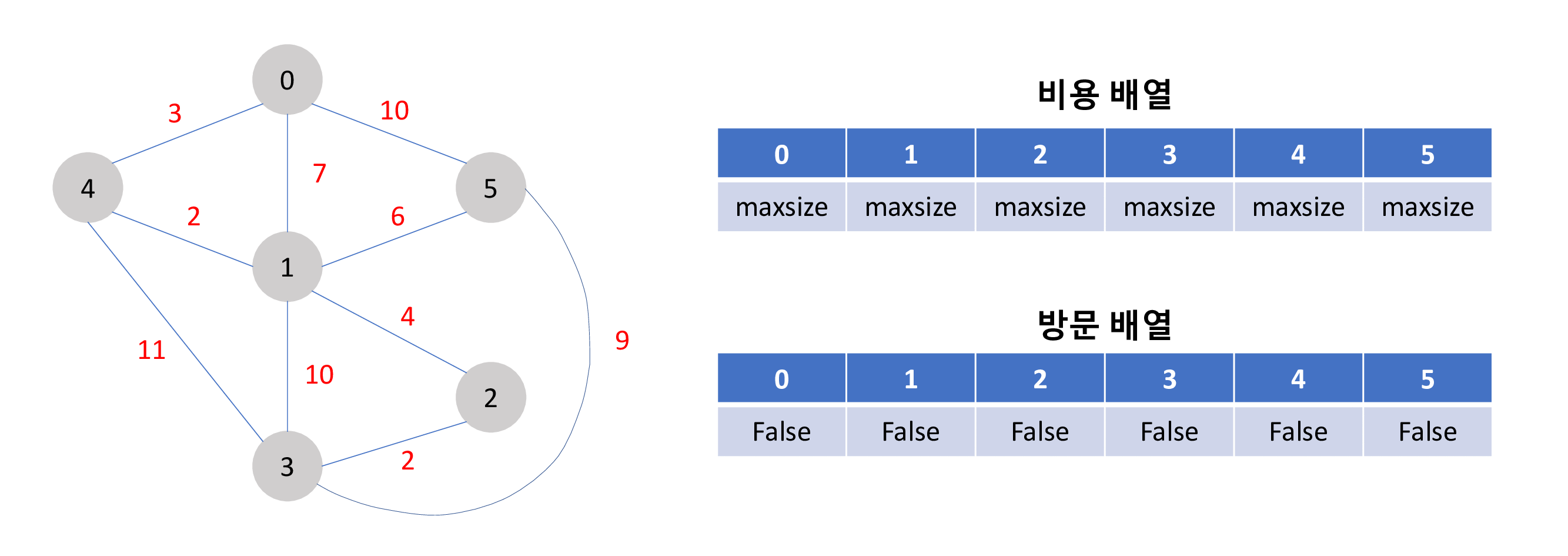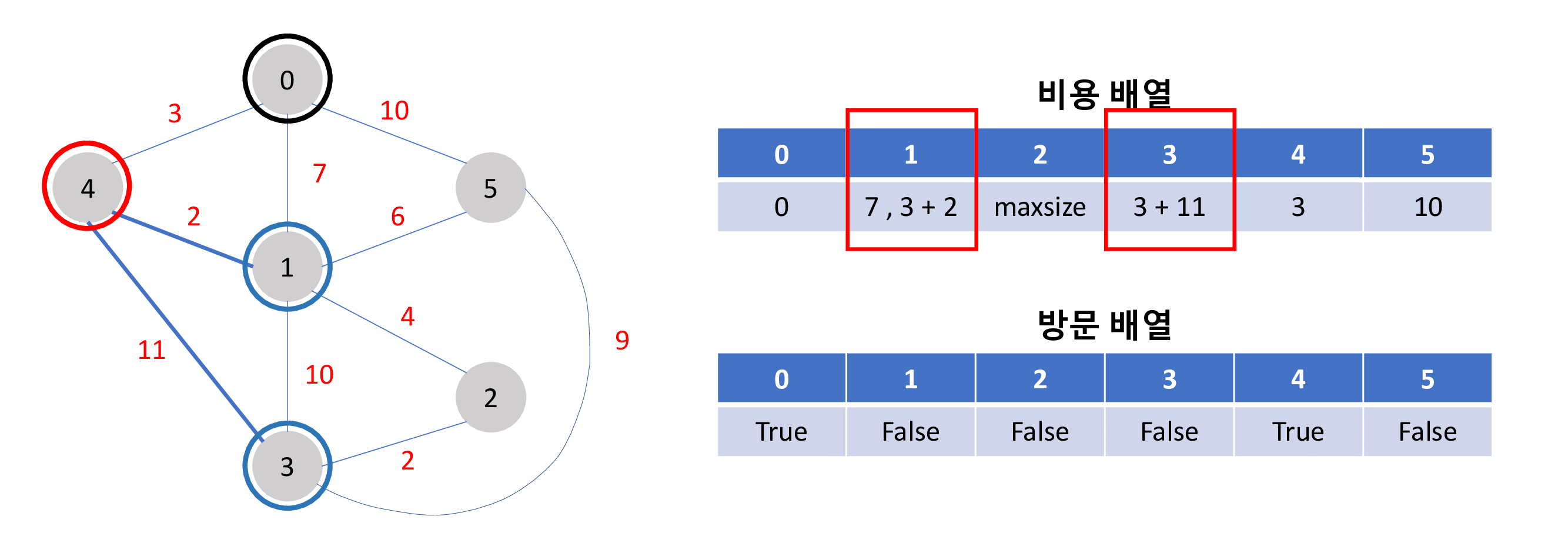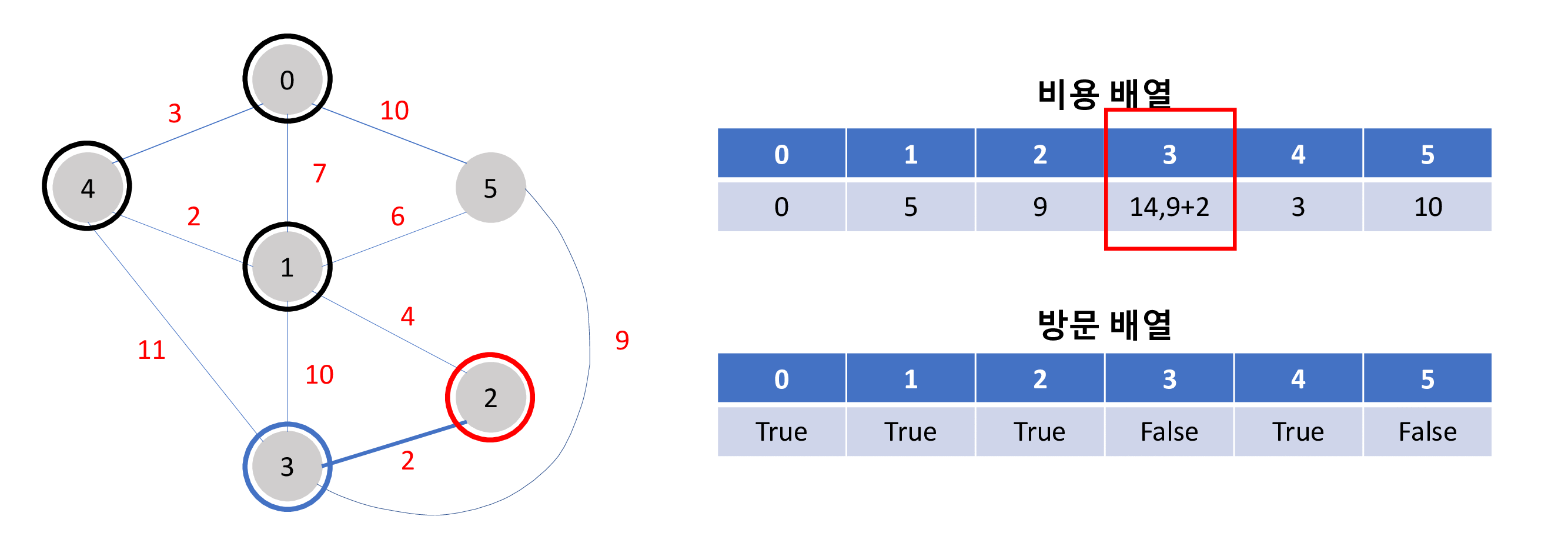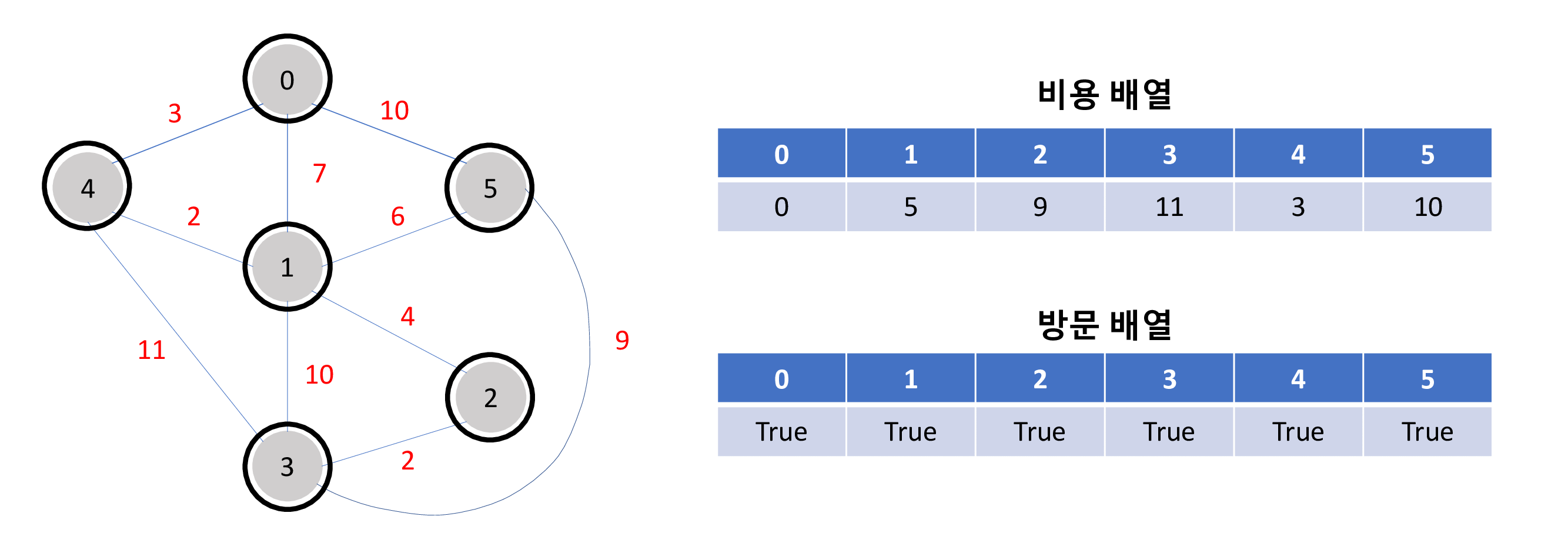
0 에서 부터 각각의 노드 까지의 최단 거리 비용은 각 비용 배열의 값이 됩니다. (예:1->2 : 5, 0->3 : 11)

다익스트라 예시코드

다익스트라를 구현 하는 예시코드는 아래와 같습니다.

visited = [False for _ in range(n)]   # 방문 배열 선언
cost = [sys.maxsize for _ in range(n)] # 비용 배열, 거리 배열 선언
visited[0] = True     # 0 번 노드를 시작점으로 설정
cost[0] = 0       
length = len(visited)
while False in visited:     # 방문하지 않은 노드가 있다면
    checkLoc = -1            # 방문하지 않은 지역 중 최솟값 찾기
    checkValue = sys.maxsize 
    for i in range(length):
        if visited[i] == False and cost[i] < checkValue:
            checkLoc = i
            checkValue = cost[i]
    if checkLoc == -1:        # 검사할 후보가 없다면 탈출
        break
    visited[checkLoc] = True
    for v1, v2, c in costs:   # 경로 완전탐색으로 비용배열 수정
        if v1 == checkLoc and visited[v2] == False:
            cost[v2] = min(cost[v2], cost[v1] + c)
        if v2 == checkLoc and visited[v1] == False:
            cost[v1] = min(cost[v1], cost[v2] + c)